- From: Neil Soiffer <soiffer@alum.mit.edu>
- Date: Tue, 6 Jul 2021 14:00:55 -0700
- To: Murray Sargent <murrays@exchange.microsoft.com>
- Cc: "ljmaher03@outlook.com" <ljmaher03@outlook.com>, "www-math@w3.org" <www-math@w3.org>
- Message-ID: <CAESRWkDvR4-Fh=xsKtHEj3_-ktrrP5Mwnqpe2YY1tAdn10Ybeg@mail.gmail.com>
Murray,
Your example means the Pearson statement is wrong and that at least in this
case, Nemeth follows presentation.
I am a little dubious that the braille produced for the 'd' ( ⠨⠈⠈⠙ ) is
correct. I'm guessing your code produced something for U+2146, which is the
&DifferentialD you use internally. I strongly suspect this is *not* what a
Nemeth reader would expect or understand even though it may be a
technically correct translation of what is there. Hopefully a Nemeth reader
will chime in.
Neil
On Tue, Jul 6, 2021 at 12:23 PM Murray Sargent <
murrays@exchange.microsoft.com> wrote:
> It’s nice when an integral ends with the ⅆ𝑥, since you know for sure
> where the integrand ends. But it’s not necessary for Nemeth braille. For
> example, the integral
>
>
>
> has the Nemeth braille
>
> ⠮⠰⠴⠘⠆⠨⠏⠐⠹⠨⠈⠈⠙⠨⠹⠌⠁⠬⠃⠀⠎⠊⠝⠀⠨⠹⠼
>
> Here the integrand is presumed to be the fraction and no more, but that is
> admittedly a heuristic. I use that heuristic both for LaTeX and for Nemeth
> braille, since OfficeMath needs to know the integrand (as does MathType).
> In MathML, it’s important to enclose the integral and the integrand in
> <mrow>’s (although I apply the heuristic to poorly formed MathML as well).
>
>
>
> Thanks,
>
> Murray
>
>
>
> *From:* Neil Soiffer <soiffer@alum.mit.edu>
> *Sent:* Tuesday, July 6, 2021 12:11 PM
> *To:* Louis Maher <ljmaher03@outlook.com>
> *Cc:* Murray Sargent <murrays@exchange.microsoft.com>; www-math@w3.org
> *Subject:* Re: [EXTERNAL] Some braille references
>
>
>
> I forgot to add in my last message that the reason I asked the question
> about integrals is because, if the Pearson statement is true, that would be
> a case of a non-presentation example of braille (because the 'dx's location
> would be different than in the presentation and hence require a little
> semantics knowledge).
>
>
>
> Neil
>
>
>
>
>
> On Tue, Jul 6, 2021 at 11:55 AM Neil Soiffer <soiffer@alum.mit.edu> wrote:
>
> In the pearson symbol site, it says this about integrals
> <https://nam06.safelinks.protection.outlook.com/?url=https%3A%2F%2Faccessibility.pearson.com%2Fresources%2Fnemeth-curriculum%2Fnemeth-symbol-library%2Findex.php%23IndefiniteIntegral&data=04%7C01%7Cmurrays%40exchange.microsoft.com%7Cdb69f0a4f2e4430c772408d940b1c46c%7C72f988bf86f141af91ab2d7cd011db47%7C0%7C0%7C637611954565150264%7CUnknown%7CTWFpbGZsb3d8eyJWIjoiMC4wLjAwMDAiLCJQIjoiV2luMzIiLCJBTiI6Ik1haWwiLCJXVCI6Mn0%3D%7C1000&sdata=v78kicPzBhRq4XQ838AeQQxV7p8Xd%2BTLufSOmDBdNnE%3D&reserved=0>
> :
>
> The integral, or indefinite integral, starts with the integral sign (dots
> 2-3-4-6). Then it is followed by the function and ends with dx.
>
>
>
> I'm dubious about this statement -- what happens when the 'dx' is in the
> numerator? I looked in the green book, and in the section about integrals,
> it only has examples where the 'dx' is at the end (also true for the APH
> tutorial). Does anyone who knows Nemeth well know the answer?
>
>
>
> Another practical bit I liked from that talk was a short description of
> "common issues in Nemeth code transcriptions" from a practitioner writing
> such materials
>
>
>
> Interesting to see that she highlights the parts that I called out in my
> original email (makes me feel like I know more than I do :-)
>
>
>
> Neil
>
>
>
>
Attachments
- image/png attachment: image003.png
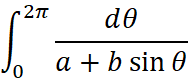
Received on Tuesday, 6 July 2021 21:01:09 UTC