- From: Yuqian Li <liyuqian@google.com>
- Date: Tue, 21 Feb 2017 13:51:27 -0500
- To: www-svg@w3.org
- Message-ID: <CACrk9yQMGGN4U-D5NOdZSK8FS6z7epGQKvFFRhCbkAtvhZu7zw@mail.gmail.com>
As https://www.w3.org/TR/SVG/filters.html#feTurbulenceElement specifies,
feTurbulence creates a Perlin turbulance, which should be uniform in all
directions (fGradient should be uniformly distributed on a ball).
However, it seems that the specific implementation (source code) in the W3C
Recommendation violates such uniformity: it directly normalizes a random
vector from [-1, -1] x [1, 1] to a unit vector (so it's uniformly
distributed on a box, rather than a ball). It generates more diagonal
gradient than horizontal/vertical ones. In Perlin's paper, it's recommended
to discard vectors with length greater than 1, and only normalizes the
remaining ones to unit vectors as the random gradient. (There are many ways
of generating uniformly random vectors on a ball; the 3rd answer in this Q/A
<http://math.stackexchange.com/questions/44689/how-to-find-a-random-axis-or-unit-vector-in-3d>
is
what's described here; it's probably the cheapest one for our 2D cases.)
For the difference, please see the attached images. In
full_original_circle.png, there are more diagonal white lines than
vertical/horizontal lines; if we rotate it by 45 degrees, we notice a
significant increase of vertical/horizontal lines and decrease of diagonal
lines in full_original_circle_45.png. On the other hand, if we properly do
the normalization (discard vectors with length greater than 1), the
full_normalize_circle.png and full_normalize_circle_45.png both have
similar number of diagonal lines and vertical/horizontal lines.
The following is the original W3C implementation:
for(k = 0; k < 4; k++)
{
for(i = 0; i < BSize; i++)
{
uLatticeSelector[i] = i;
for (j = 0; j < 2; j++)
fGradient[k][i][j] = (double)(((lSeed = random(lSeed)) %
(BSize + BSize)) - BSize) / BSize;
s = double(sqrt(fGradient[k][i][0] * fGradient[k][i][0] +
fGradient[k][i][1] * fGradient[k][i][1]));
fGradient[k][i][0] /= s;
fGradient[k][i][1] /= s;
}
}
And here's the properly normalized implementation that generates gradient
uniformly in all directions:
for(k = 0; k < 4; k++)
{
for(i = 0; i < BSize; i++)
{
uLatticeSelector[i] = i;
for (j = 0; j < 2; j++)
fGradient[k][i][j] = (double)(((lSeed = random(lSeed)) %
(BSize + BSize)) - BSize) / BSize;
s = double(sqrt(fGradient[k][i][0] * fGradient[k][i][0] +
fGradient[k][i][1] * fGradient[k][i][1]));
if (s > BSize) {
i--; // discard the current random vector; try it again.
continue;
}
fGradient[k][i][0] /= s;
fGradient[k][i][1] /= s;
}
}
Thanks,
Yuqian
Attachments
- image/png attachment: full_original_circle.png

- image/png attachment: full_original_circle_45.png
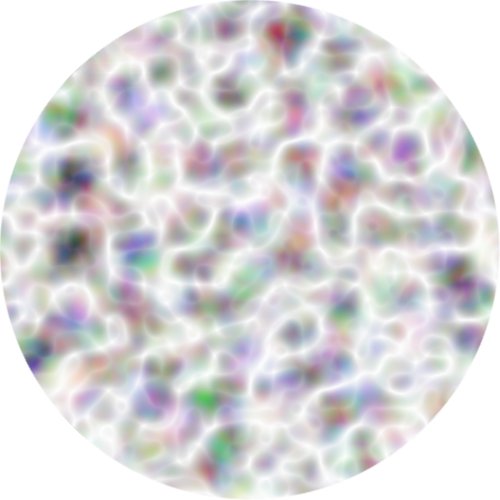
- image/png attachment: full_normalize_circle.png
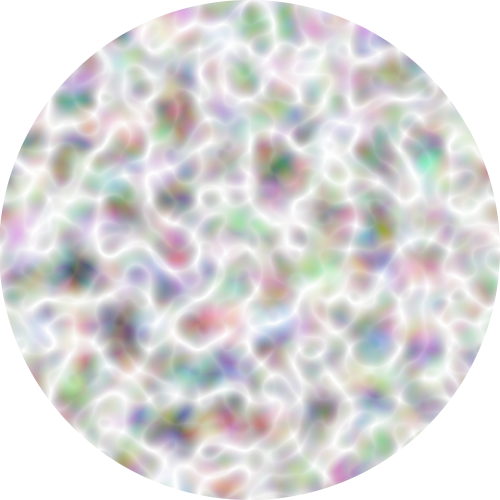
- image/png attachment: full_normalize_circle_45.png

Received on Tuesday, 28 February 2017 22:25:07 UTC