- From: Jeremie Patonnier <jeremie.patonnier@gmail.com>
- Date: Sun, 23 Sep 2012 18:29:17 +0200
- To: "Tab Atkins Jr." <jackalmage@gmail.com>
- Cc: www-svg <www-svg@w3.org>
- Message-ID: <CAEi838=qsJE5XFtwigdkWacjw9bXQghMJgYKFe3aXe3q1Rvg1w@mail.gmail.com>
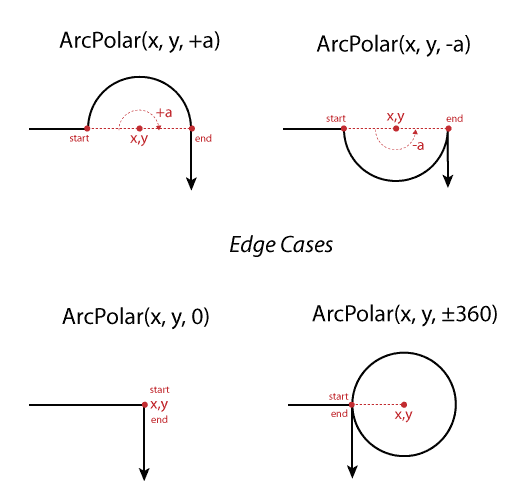
Hi, As a web developer, I like any improvement in the way to define Arc that can make author life easier. I really like Tab's proposal but, IMO, one of the hardest thing with all the arc definitions is the definition of the end point of the arc. It requires to perform some trigonometry with sin and cos function to calculate the coordinates of that end point. For many web authors, this is amazingly painful (yes, I'm serious) So, I wish to suggest another possible arc definition: We could call it "ArcPolar", it will take the following parameters: - An x,y value that define the center of the circle that include the arc - An angle (express in degree) that will define the position of the end point of the arc. A positive angle draw the arc clockwise and a negative angle draw the arc anti-clockwise. Because I'm not that good to explain correctly the result of such an arc definition, here is an image with some common case (a good schema worth thousands of words) [image: Images intégrées 1] There is a few edge cases : 1. ArcPolar(x, y, 0) is a zero length segment 2. ArcPolar(x, y, ±360) define a non-closed circle (visually, it's a circle but it's also an non-closed path) 3. If the center of the circle that include the arc match the starting point, the resulting arc is a zero length segment 4. If the value of the angle is out of the range -360/360, it's considered as follow: angle = angle mod 360 This is a very simple and very easy way for authors to define arcs. Actually, at worth, it make the definition of simple arc such 90deg or 180deg arc way much easier, but the biggest use case I have in mind is the production of pie charts or donut charts. With such an arc definition, it become easy to write path with arc by hand without using any authoring tool. IMO it will help in many HTML+SVG document. Best regards, -- Jeremie ............................. Web : http://jeremie.patonnier.net Twitter : @JeremiePat <http://twitter.com/JeremiePat> 2012/9/20 Tab Atkins Jr. <jackalmage@gmail.com> > This discharges my action-3388. > > Near the end of the f2f yesterday, Dirk pointed us to Paper.js, to > look at some of their details around paths. One thing that > immediately jumped out was one of the overloads for their "arcTo()" > function, which takes an implicit startpoint, an endpoint, and a third > point, and defines a circular arc that intersects the third point. > This immediately seemed like a convenient functionality, as it lets > you easily describe arcs that are tangent to another shape, or that > can be easily sized with mouse interaction. This seems to meet our > goal of adding things that are useful and reduce the need to do trig > just to write a path. > > So, I'm officially proposing this for inclusion in the <path> syntax. > We can call it "ArcThrough", and it takes 4 arguments - an x,y pair > for the pass-through point, and an x,y pair for the end point. You > don't need to specify a radius or anything, as the circle is already > uniquely specified by the three points: > <http://paulbourke.net/geometry/circlefrom3/>. > > There are three degenerate cases that need special attention: > > 1. When the "through" point is colinear with the start and end points. > This one is really easy because it just defines a circle with > infinite radius, which usually goes by the name "line". If the > "through" point is between the other two, it devolves to a lineTo > between the start and end point; if the "through" point is on either > end of the other two, it's the infinite line through those two points, > minus the segment connecting them. > > 2. When the "through" point is coincident with the start or end point: > This devolves into defining a circle from two points, for which there > are infinite solutions. I propose we define this as producing the > smallest such circle, which has its center exactly between the start > and end points. (Note that there's a slight difficulty here - any > solution you choose will produce a discontinuity for many directions, > as the command's results are unstable (large output changes from small > input changes) when the "through" point closely approaches one of the > endpoints. > > 3. When the start and points are coincident. This again devolves into > defining a circle from two points, but it potentially has different > constraints on its solution, since it's constrained to start and end > on those points. I propose we take the same solution as (2) - it > defines a full circle with its center exactly between the start/end > point and the "through" point. This avoids any discontinuities, since > as the start and end points approach each other, the arc approaches > this form. This also happens to give you an interesting unexpected > ability - you can do gui drawing of circles *really* easy by clicking > on a point you want the circle to start from and then dragging to > where you want it to end, and creating a path with start/end points > both set to the mousedown coord and the "through" point set to the > mousemove coord. > > ~TJ > >
Attachments
- image/png attachment: arc-polar.png
Received on Sunday, 23 September 2012 16:30:07 UTC