- From: Henry Story <henry.story@bblfish.net>
- Date: Sun, 30 Jul 2006 15:52:55 +0200
- To: Semantic Web <semantic-web@w3.org>
- Message-Id: <F9DA499D-9528-4ACE-8893-42B95E2D9AF7@bblfish.net>
I have just written a longer entry on the relationship between RDF and Metcalf's law. here: http://blogs.sun.com/roller/page/bblfish? entry=rdf_and_metcalf_s_law -------------------- RDF and Metcalf's law
I am trying to find a way of adapting Metcalf's law to the Semantic Web.
My initial intuition is that something like this is true:
"the value of your information grows exponentially with your ability
to combine it with new information."
Illustration
To illustrate and ground this intuition consider the following
example. In OSX I can enter information about people I know into the
AddressBook application. I can add information about where they live,
what their email address is, a chat account name, a photo, and much
more... So it does pretty much what a paper address book would do,
except that it can easily be copied, backed up, and searched. Those
are minor advantages though, compared with what I wish to highlight
here.
When I read an email with Mail.app, it will display the picture of
the sender, taken from my Address Book. (iChat has similar
functionality). Furthermore if someone I know is online, I will see a
little sign appear in my Mail application next to any emails from
that person. These features makes my online life a lot more pleasant.
The application is combining information about who the mail is from,
with information in the address book, and information from the chat
application. The information in the address book is therefore much
more valuable than it would be in a paper version. It can be much
more easily combined with new information.
Information and Semantics
One's ability to combine information is related to one's ability to
understand it. Most importantly: in order for information to be
combined one has to also be able to tell when two pieces of
information are referring to the same thing, so that one can relate
information about something that we have in one store to information
about the same thing that we have in another store. In the example I
gave above, the information is an email address, an aim chat account,
its relation to a depiction which all describe a Person, and the
metadata from an email which comes from that same Person.
Unsurprisingly in both of these cases our ability to resolved this
identity came from the use of a URI (email addresses are URIs). URIs
are universal names for things, easily created, and easily parsed.
The closer one is to having a mechanical method to finding identity,
the faster one will be able to combine information, and so of course
the greater one's ability to do so.
Compare this to the situation with old fashioned tabular database.
Data in such a store can be very usefully combined and related, for
those people who set it up, since they understand and control the
meaning of the schemas (see an earlier article on Business
Intelligence). But relating data from one database to that in another
is not simple at all. One has to extract the semantics hidden in each
database ("what do these tables refer to?") by looking perhaps at how
the data has or is being used. This work of creating correlation
between the tables in each database is slow and complicated, and
needs to be done for each pairs of databases again and again. And so
this severely hinders one's ability to combine data. In a sense, old
tabular databases are good at storing data, not good at helping one
re-use that data and transform it.
Now since one can only relate information when one knows it to be
referring to the same thing, it is clear that it is the semantics of
the information that we are interested in. In other words it is
semantics that is essential to one's ability to combine information.
Which is what the Resource Description Framework (RDF) provides.
The law
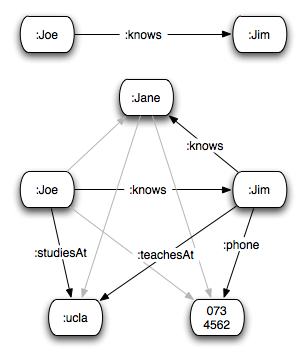
RDF is a framework that uses the property of URIs to be able to name anything (hence also relations) to allow one to form a graph of information. By naming things and stating the relations between them we can create a graph. By publishing this graph we can add those relations to the worldwide graph of information about things. We can therefore think of a piece of information both as an edge of the graph and as an RDF sentence. The objects are the nodes of the graph. The relations are the arrows between them. We may not always be able to relate one thing directly to another using a known relation, but given an indirect relation between two things we can infer a new direct inferred relation between those two things. To illustrate, given the sentences :Joe :knows :Jim . :Jim :knows :Jane . we can infer that there is also a direct inferred relationship between :Joe and :Jane. We can now apply Metcalf's law. As the number of objects in a graph increases, so the number of direct and indirect relations between the objects in the graph increases. But it increases a lot faster than Metcalf's law. Because in RDF two object can have any number of relations between each other. So :Joe :knows :Jim but perhaps also :Joe :livesWith :Jim, and :Joe :tallerThan :Jim. We can think of Metcalf's law as a special case of our law, where there is only one type of symmetrical relation (:isLinkedTo). Or we can count the RDF relations as objects and work with Metcalf's law, with a restriction that Metcalf links between relations always have to first go through a relation object first. In any case as the number of connected objects in a graph grows so the number of relations between those objects grows a lot faster. So if you take a graph of information that is private and add it to the public graph of information you immediately add a huge number of potential new links to that graph. The number of links of the public graph has grown, but the number of links to the object on the previously private graph has grown a lot faster, since all the publically available information can now relate it. Value How is this related to value then? One very simple relation to value has to do with the value of the objects (be they products, thoughts, blogs, whatever), which we describe. As we add our information to the huge pool of information, we can help others discover something new about our objects which will increase their interest in them, which increases their value as per the law of Supply and demand. By making our information public using RDF, we make it easy for others to build new services by combining our information with other information, so as to direct new interest towards our objects. The new service providers can be thought of as specialised inference engines that will create new relations to our objects for the audience that they serve. Notes It would be nice to ground this law more precicely mathematically. Feedback on improovements welcome :-) The OSX example is also good because it points out a deficiency of not working with RDF. The schema defined by vCards is very limited. There is no way of adding a new well understood relation between a person and their blog page, foaf page, who someone knows, or what someone likes. The API for querying the AddressBook information is also completely ad hoc, which must be part of the reason why other non Apple apps on OSX don't make such good use of the information. Imagine all of this information was instead stored in a central RDF database (a SpotLight successor perhaps) queriable via SPARQL. This would mean that all apps could make use of the same information, and it would be easy to add new types of information.
Attachments
- image/png attachment: 2006_07_29_14-09-17-155_n3.small.png
- image/jpeg attachment: 2006_07_30_13-58-31-855_n0.jpg
Received on Sunday, 30 July 2006 13:53:15 UTC