Jeremy Carroll
One approach to containers in RDF is to start off with what we've got (Bag, Seq, Alt, and daml:collection) all of which suffer from semantic (and syntactic) problems; and to try and fix some of the problems.
In contrast, this paper tries to design a good solution to containers and then tries to work out how much of that good solution can be used within RDF1 - particularly given the requirement not to ignore the needs reflected by the existence of daml:collection.
rdf:Seq, rdf:Bag, rdf:Alt and daml:collection point to a variety of container needs:
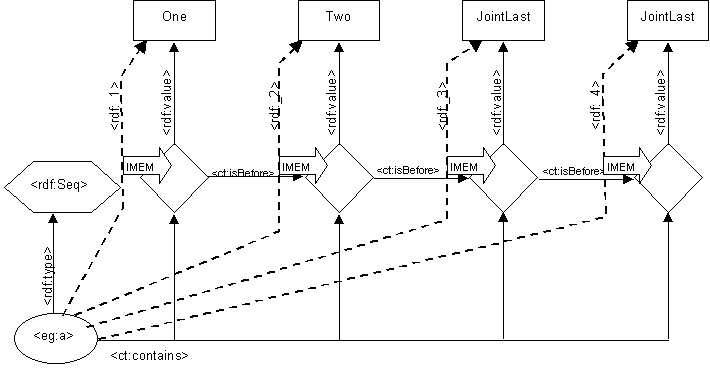
The proposal in this paper is to achieve these goals using a layer of indirection. An example bag is:
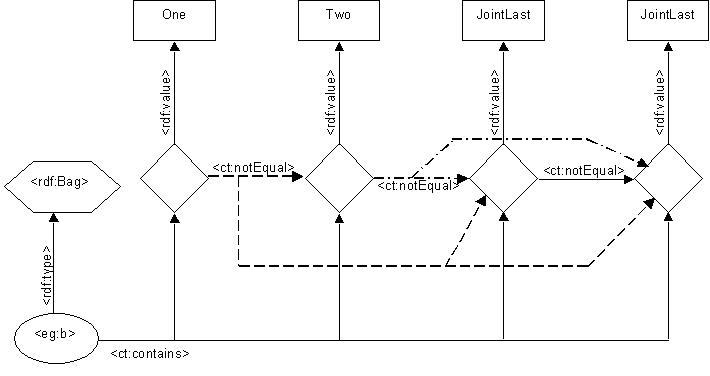
This could correspond with:
<rdf:Bag rdf:about="http://example.org/#b"> <rdf:li>One</rdf:li> <rdf:li>Two</rdf:li> <rdf:li>JointLast</rdf:li> <rdf:li>JointLast</rdf:li> </rdf:Bag>
We see that the lexical nodes in the container are
no longer directly linked from the container node at all.
Instead there is an indirection. The container links to
additional blank nodes (shown as diamonds) with the new
<ct:contains> arcs, and each blank node
as an <rdf:value> arc linking
from it to the member.
The diamond nodes are used to represent what it is that we know about the relationships between the container members.
For the rdf:Bag we know that all the members
are distinct. This is shown by the <ct:notEqual>
arcs.
The multiset aspect of the Bag, i.e. that its members can have multiplicity
greater than one, is reflected by the JointLast element.
Even if there were only one JointLast node with two
<rdf:value> arcs linking to it, we would still
see the multiplicity of two because the two diamonds are required to
be distinct due to the (special) semantics of <ct:notEqual>
that they are.
In a true set, no such constraint is known:

Now, we cannot tell that this is different from the similar:
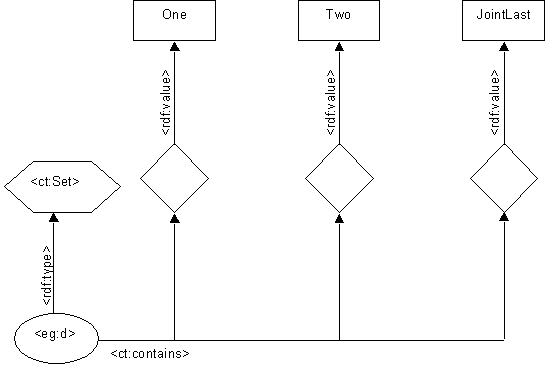
because the two graphs mutually entail one another, by the RDF model theory.
Note that in the Bag figure, symmetric <ct:notEqual>
arcs were omitted. This was simply for clarity of the figure. The special semantics
of inequality is symmetric, and so the shown figure mutual entails one in which the
<ct:notEqual> arcs all point the other way, or both ways.
To show a sequence we need to add partial order information (instead of inequality).
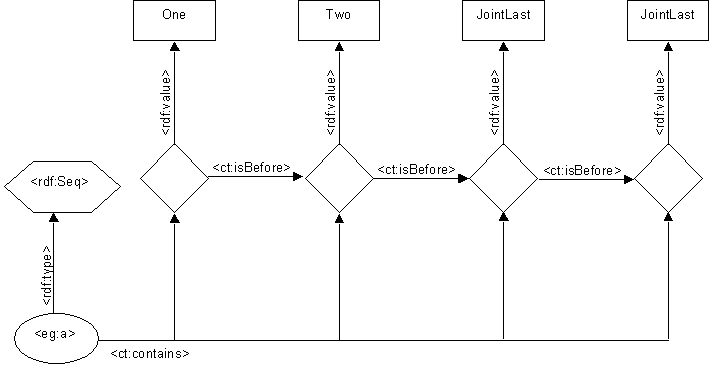
The <ct:isBefore> arcs show this information.
Since this is a strict inequality, these arcs entail (the meaning of)
<ct:notEqual> arcs. Also since the semantics of
<ct:isBefore> we have omitted many additional edges that could
have been included.
Note that unlike <daml:rest>, <ct:isBefore>
does not take unique values. The diamond linking to "One" is <ct:isBefore>
all the other diamonds.
Alt
Surpisingly, it is possible to rearticulate M&S <rdf:Alt> in this
framework, as a container with a first element, but otherwise being a bag.
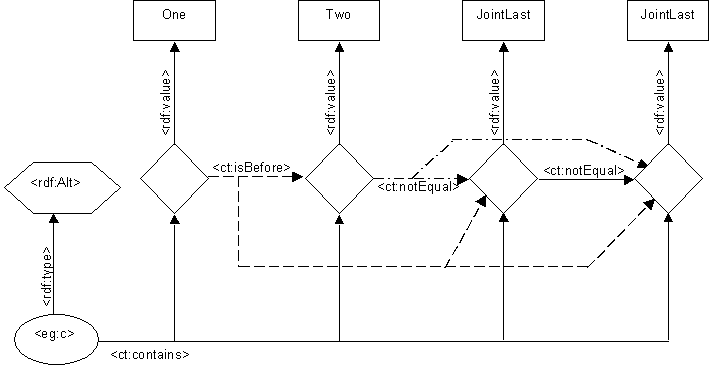
We do not capture the suggestion from M&S that an Alt reflects a choice (OR)
while a Bag reflects an AND.
In fact, the way that other triples, with the container as object,
treat the container, is undefined by this document (and the RDF Model Theory).
To consider two examples, a mailing list using a Bag to list the members,
in most cases the practical interpretation will be to send to mail to all the members.
Whereas a download site described using an Alt to describe its
primary location and then some mirror sites, is practically interpreted as downloading the
software from any one of the collection. (Thorough integrity checking of the site requires
looking at all the mirrors, for example after a recent virus attack).
In the logical (model theoretic) interpretation being discussed here, it is not inappropriate
to use conjunctive semantics despite the variety of practical activities that we are describing.
This proposal embeds a stronger open world assumption than is present in RDF M&S. In particular, it is possible to insert elements into the middle of a sequence, as well as adding elements to the end of a sequence.
This also contrasts with daml:collection in which the
<daml:rest> property is a successor relationship rather
than merely an order relationship. (i.e. if
a <daml:rest> b .
then we know that there is nothing in between a and b).
Hence unlike in DAML, the notion of end-marker is incoherent in this proposal.
The suggestion in this proposal is to use a <ct:size property
whose object is a string labelled node interpreted as an xsd:integer.
This size refers to the number of resources in the collection at the first level (i.e. the diamonds in the diagrams) rather than the second level.
Both <ct:notEqual> and <ct:isBefore
are irreflexive.
These edges are implicit when the type of the container is
rdf:Bag, rdf:Seq or rdf:Alt.
Hence it is possible to close a container by setting the size to the number of
explicitly enumerated
elements in the container.
This also allows the embedding of contradiction in RDF/XML e.g.
<rdf:Bag rdf:about="http://example.org/#b" ct:size="3"> <rdf:li>One</rdf:li> <rdf:li>Two</rdf:li> <rdf:li>JointLast</rdf:li> <rdf:li>JointLast</rdf:li> </rdf:Bag>
We note that this is inherent in the ability
to close containers.
(e.g.
<daml:nil> <daml:rest> _:a .
is a contradiction).
It is possible to use this approach to containers within RDF as defined by M&S. This consists
of additions to the model theory, in particular, the concept of an
interpretation with containers
, a concept of entailment with containers
and closure rules for containers
.
An interpretation with containers is an RDFS interpretation as defined by the
RDF Model theory; subject to some additional conditions.
The interpretation is defined along with an additional interpretation
partial function
IMEM, whose domain is the edges of the schema closure
of the RDF graph.
IMEM is defined on edges whose property is one of the
container membership properties.
The range of IMEM is the universe of discourse.
It can be thought of as introducing a new blank node for each
rdf:_iii edge.
Most of the additional conditions concern some pair of asserted triples E and E'
s rdf:_iii o . s rdf:_jjj o' .
E and E' are found in the schema closure.
We also use iii and jjj to refer to the relevant integer values.
Notice this means that the following table of conditions is countably infinite, with entries
generated by each pair of integers.
(Note that E and E' have the same subject but possibly
different objects).
| If E is an asserted triple then <I(s),IMEM(E)> is in IEXT(I(ct:contains)) and <IMEM(E),I(o)> is in IEXT(I(rdf:value)). |
|
If E and E' are asserted triples and iii<jjj and I(s) is in one or more of ICEXT(rdf:Bag) or ICEXT(rdf:Alt) or ICEXT(rdf:Seq) then <IMEM(E),IMEM(E')> is in IEXT(I(ct:notEqual)). |
|
If E and E' are asserted triples and iii<jjj and
I(s) is in ICEXT(rdf:Seq) then <IMEM(E),IMEM(E')> is in IEXT(I(ct:isBefore)). |
|
If E and E' are asserted triples and iii=1, jjj>1 and
I(s) is in ICEXT(rdf:Alt) then <IMEM(E),IMEM(E')> is in IEXT(I(ct:isBefore)). |
| IEXT(I(ct:notEqual)) is irreflexive. (i.e. if <x,y> is in IEXT(I(ct:notEqual)) then x is not equal to y.). |
| IEXT(I(ct:isBefore)) is transitive and irreflexive. |
|
If <s,o> is in IEXT(I(ct:size)) then o is in the lexical space of xsd:integer; and the corresponding integer is the size of { x : <s,x> is in IEXT(I(ct:contains)) }. |
As might be expected, it is possible to express the constraints on an interpretation
in terms of closure rules. This act on the
RDF graph formed by using the schema closure rules.
However, it is made a little tricky by the
behaviour of the IMEM interpretation function.
We need to include a corresponding function in the closure rules.
This function is called GENSYM and its domain is the set of
triples in the schema closure, and its range is a new set
of blank nodes, not in the schema closure.
GENSYM is bijective, so that each new blank node
unambiguously determines a corresponding edge in the schema closure.
| 1 | xxx rdf:_iii yyy . |
xxx ct:contains GENSYM(xxx rdf:_iii yyy) . GENSYM(xxx rdf:_iii yyy) rdf:value rdf:_iii yyy . |
| 2a |
xxx rdf:type rdf:Bag . xxx rdf:_iii yyy . xxx rdf:_jjj zzz . where not iii = jjj |
GENSYM(xxx rdf:_iii yyy) ct:notEqual GENSYM(xxx rdf:_jjj zzz) . |
| 2b |
xxx rdf:type rdf:Alt . xxx rdf:_iii yyy . xxx rdf:_jjj zzz . where not iii = jjj |
GENSYM(xxx rdf:_iii yyy) ct:notEqual GENSYM(xxx rdf:_jjj zzz) . |
| 3 |
xxx rdf:type rdf:Seq . xxx rdf:_iii yyy . xxx rdf:_jjj zzz . iii < jjj |
GENSYM(xxx rdf:_iii yyy) ct:notEqual GENSYM(xxx rdf:_jjj zzz) . GENSYM(xxx rdf:_jjj yyy) ct:notEqual GENSYM(xxx rdf:_iii zzz) . GENSYM(xxx rdf:_iii yyy) ct:isBefore GENSYM(xxx rdf:_jjj zzz) . |
| 4 |
xxx rdf:type rdf:Alt . xxx rdf:_1 yyy . xxx rdf:_jjj zzz . 1 < jjj |
GENSYM(xxx rdf:_1 yyy) ct:isBefore GENSYM(xxx rdf:_jjj zzz) . |
Checking the size constraints on closed containers is done after applying the above closure rules.
The first rule is that for all
xxx ct:size yyy .
yyy must be in the lexical space of xsd:integer.
The size constraint fails if there are any set of edges matching the following conditions
xxx ct:size sss . with sss a literal corresponding to the integer n xxx ct:contains zzz_1 . xxx ct:contains zzz_2 . ... xxx ct:contains zzz_n . xxx ct:contains zzz_[n+1] . And for all i not equal to j, with 1 <= i != j <= n+1 zzz_i ct:notEqual zzz_j .
i.e. The first triple has object sss equal to n
and there are n+1 following triples starting xxx ct:contains,
and for each (n2+n) pair of objects of those triples the
triple with the first as subject, the second as object and the predicate being
ct:notEqual.
Entailment is more difficult than for RDF and RDFS.
The problem is that the entire semantics of the rdf:_iii
properties has been encoded in the new approach to containers. The intent
is that the rdf:_iii properties are now irrelevant.
In terms of the closure rules, this corresponds to a final non-monotonic step of
discarding all the triples with an rdf:_iii predicate.
Also all triples of the form:
rdf:_iii rdf:type rdfs:Property .
are discarded.
We can now make the normal syntactic comparisons between the two graphs (subgraph isomorphism) to determine entailment.
To achieve the same result model theoretically we will
divide those parts of the interpretation to do with
the rdf:_iii properties from the rest of
the interpretation.
A membership-free interpretation I* is defined on a vocabulary V of URIs. I* is defined by:
An RDF Interpretation I (given by IR, IEXT, IS) is an extension of a membership-free interpretation if and only if whenever v in V is such that IEXT(IS(v)) is not equal to IEXT*(IS(v)) then v is an rdf:_iii.
A membership-free interpretation I* satisfies a graph E if there exists an RDF interpretation I, extending I*, which satisfies E, the semantic conditions both of RDFS and of interpretations with containers.
In other words, I* is everything an RDF interpretation is except for how the rdf:_iii correspond to properties, and any such correspondence can be used to check whether I* satisfies any particular graph.
A membership free interpretation is in some sense existentially quanitificatied over the exact interpretation of the rdf:_iii properties, while leaving the new two level model of partially ordered containers unchanged.
We note that, before we get onto entailment, there is a small technical glitch concerning the vocabularies V. Let us consider the two RDF graphs, of one triple each:
<foo> <rdf:_1> "bar" .
<foo> <rdf:_2> "bar" .
One of the goals of this document is to show how we can read these as entailing each other, because both are using RDF containers, and so in both <foo> is a container with one element "bar". However, the minimum vocubulary required to read is not sufficient to read the second. Thus for entailment purposes we need to restrict the interpretations we consider to those over a wider enough vocabulary for all the graphs in the entailments. We will use the word "relevant" to indicate this.
A set S of RDF graphs c-entails E if every relevant membership-free interpretation which satisfies every member of S also satisfies E.
Note that when there are two premises then the interpretation of the property corresponding to rdf:_1 in the first and its interpretation in the second generally differ.
Taking subproperties of rdf:_iii may lead to surprising results. It can be used as a technique to force the use of particular rdf:_iii properties, making c-entailment closer to RDF-entailment. If we have a subproperty of two different rdf:_iii properties, or declare that rdf:_iii is a sub property of rdf:_jjj we may get very surprising results concerning closed containers.
These are sample test cases for c-entails. Most of the time, these entailments fail as RDF entailments.
<rdf:Bag rdf:about="http://example.org/#b"> <rdf:li>One</rdf:li> </rdf:Bag>
<rdf:Bag rdf:about="http://example.org/#b"> <rdf:_2>One</rdf:_2> </rdf:Bag>
<rdf:Seq rdf:about="http://example.org/#b"> <rdf:li>One</rdf:li> </rdf:Seq>
<rdf:Seq rdf:about="http://example.org/#b"> <rdf:_2>One</rdf:_2> </rdf:Seq>
<rdf:Bag rdf:about="http://example.org/#b"> <rdf:li>One</rdf:li> <rdf:li>Two</rdf:li> </rdf:Bag>
<rdf:Bag rdf:about="http://example.org/#b"> <rdf:li>Two</rdf:li> <rdf:li>One</rdf:li> </rdf:Bag>
<rdf:Seq rdf:about="http://example.org/#b"> <rdf:li>One</rdf:li> <rdf:li>Two</rdf:li> </rdf:Seq>
<rdf:Seq rdf:about="http://example.org/#b"> <rdf:_10>Two</rdf:_10> <rdf:_5>One</rdf:_5> </rdf:Seq>
<rdf:Seq rdf:about="http://example.org/#b"> <rdf:li>One</rdf:li> <rdf:li>Two</rdf:li> </rdf:Seq>
<rdf:Seq rdf:about="http://example.org/#b"> <rdf:li>Two</rdf:li> <rdf:li>One</rdf:li> </rdf:Seq>
<rdf:Alt rdf:about="http://example.org/#b"> <rdf:li>One</rdf:li> <rdf:li>Two</rdf:li> </rdf:Alt>
<rdf:Alt rdf:about="http://example.org/#b"> <rdf:_10>Two</rdf:_10> <rdf:_5>One</rdf:_5> </rdf:Alt>
<rdf:Bag rdf:about="http://example.org/#b" ct:size="2"> <rdf:li>One</rdf:li> <rdf:li>Two</rdf:li> </rdf:Bag>
<rdf:Bag rdf:about="http://example.org/#b"> <rdf:li>Two</rdf:li> </rdf:Bag>
<rdf:Bag rdf:about="http://example.org/#b" ct:size="2"> <rdf:li>One</rdf:li> <rdf:li>Two</rdf:li> </rdf:Bag>
<rdf:Bag rdf:about="http://example.org/#b" ct:size="1"> <rdf:li>Two</rdf:li> </rdf:Bag>
<rdf:Bag rdf:about="http://example.org/#b"> <rdf:li>One</rdf:li> <rdf:li>Two</rdf:li> <rdf:li>Three</rdf:li> </rdf:Bag>
<rdf:Bag rdf:about="http://example.org/#b" > <rdf:li>One</rdf:li> <rdf:li>Three</rdf:li> </rdf:Bag>
<rdf:Bag rdf:about="http://example.org/#b"> <rdf:li>One</rdf:li> <rdf:li>Two</rdf:li> <rdf:li>Three</rdf:li> </rdf:Bag>
<rdf:Seq rdf:about="http://example.org/#b"> <rdf:li>One</rdf:li> <rdf:li>Two</rdf:li> <rdf:li>Three</rdf:li> <rdf:li>Four</rdf:li> </rdf:Seq>
<rdf:Seq rdf:about="http://example.org/#b"> <rdf:li>One</rdf:li> <rdf:li>Two</rdf:li> </rdf:Seq>
<rdf:Seq rdf:about="http://example.org/#b"> <rdf:li>Three</rdf:li> <rdf:li>Four</rdf:li> </rdf:Seq>
<rdf:Seq rdf:about="http://example.org/#b"> <rdf:li>Two</rdf:li> <rdf:li>Four</rdf:li> </rdf:Seq>
<rdf:Seq rdf:about="http://example.org/#b"> <rdf:li>One</rdf:li> <rdf:li>Two</rdf:li> </rdf:Seq>
<rdf:Seq rdf:about="http://example.org/#b"> <rdf:li>Three</rdf:li> <rdf:li>Four</rdf:li> </rdf:Seq>
<rdf:Seq rdf:about="http://example.org/#b"> <rdf:li>Two</rdf:li> <rdf:li>Four</rdf:li> </rdf:Seq>
<rdf:Seq rdf:about="http://example.org/#b"> <rdf:li>One</rdf:li> <rdf:li>Two</rdf:li> <rdf:li>Three</rdf:li> <rdf:li>Four</rdf:li> </rdf:Seq>
<rdf:Seq rdf:about="http://example.org/#b"> <rdf:li>One</rdf:li> <rdf:li>Two</rdf:li> </rdf:Seq>
<rdf:Seq rdf:about="http://example.org/#b"> <rdf:li>Two</rdf:li> <rdf:li>Three</rdf:li> </rdf:Seq>
<rdf:Seq rdf:about="http://example.org/#b"> <rdf:li>One</rdf:li> <rdf:li>Two</rdf:li> <rdf:li>Three</rdf:li> </rdf:Seq>
<rdf:Seq rdf:about="http://example.org/#b"> <rdf:li>One</rdf:li> <rdf:li>Two</rdf:li> </rdf:Seq>
<rdf:Seq rdf:about="http://example.org/#b"> <rdf:li>Three</rdf:li> <rdf:li>Four</rdf:li> </rdf:Seq>
<rdf:Seq rdf:about="http://example.org/#b"> <rdf:li>One</rdf:li> <rdf:li>Two</rdf:li> </rdf:Seq> <rdf:Seq rdf:about="http://example.org/#b"> <rdf:li>Three</rdf:li> <rdf:li>Four</rdf:li> </rdf:Seq>
<rdf:Seq rdf:about="http://example.org/#b"> <rdf:li>One</rdf:li> <rdf:li>Four</rdf:li> </rdf:Seq> <rdf:Seq rdf:about="http://example.org/#b"> <rdf:li>Three</rdf:li> <rdf:li>Two</rdf:li> </rdf:Seq>
<rdf:Seq rdf:about="http://example.org/#b"> <rdf:li>One</rdf:li> <rdf:li>Two</rdf:li> </rdf:Seq> <rdf:Seq rdf:about="http://example.org/#b"> <rdf:li>Three</rdf:li> <rdf:li>Four</rdf:li> </rdf:Seq>
<rdf:Seq rdf:about="http://example.org/#b"> <rdf:li>One</rdf:li> <rdf:li>Two</rdf:li> </rdf:Seq>
<rdf:Seq rdf:about="http://example.org/#b"> <rdf:li>Three</rdf:li> <rdf:li>Four</rdf:li> </rdf:Seq>
<rdf:Seq rdf:about="http://example.org/#b"> <rdf:li>One</rdf:li> <rdf:li>Four</rdf:li> </rdf:Seq>
<rdf:Seq rdf:about="http://example.org/#b"> <rdf:li>Three</rdf:li> <rdf:li>Two</rdf:li> </rdf:Seq>
<rdf:Seq rdf:about="http://example.org/#b"> <rdf:li>One</rdf:li> <rdf:li>Two</rdf:li> </rdf:Seq> <rdf:Seq rdf:about="http://example.org/#b"> <rdf:li>Three</rdf:li> <rdf:li>Four</rdf:li> </rdf:Seq>
<rdfs:Property rdf:ID="first"> <rdfs:subPropertyOf rdf:resource="http://www.w3.org/...#_1"/> </rdfs:Property> <rdf:Bag rdf:about="http://example.org/#b"> <eg:first>One</eg:first> <rdf:_2>Two<rdf:_2 </rdf:Bag>
<rdf:Bag rdf:about="http://example.org/#b"> <rdf:li>Two</rdf:li> <rdf:li>One</rdf:li> </rdf:Bag>
<rdfs:Property rdf:ID="first"> <rdfs:subPropertyOf rdf:resource="http://www.w3.org/...#_1"/> </rdfs:Property> <rdf:Bag rdf:about="http://example.org/#b"> <eg:first>One</eg:first> <rdf:_2>Two<rdf:_2 </rdf:Bag>
<rdfs:Property rdf:ID="first"> <rdfs:subPropertyOf rdf:resource="http://www.w3.org/...#_1"/> </rdfs:Property> <rdf:Bag rdf:about="http://example.org/#b"> <rdf:li>Two</rdf:li> <rdf:li>One</rdf:li> </rdf:Bag>
<eg:Set rdf:about="http://example.org/#b"> <rdf:li>One</rdf:li> <rdf:li>One</rdf:li> </eg:Set>
<eg:Set rdf:about="http://example.org/#b"> <rdf:_23>One</rdf:_23> </eg:Set>
<rdf:Bag rdf:about="http://example.org/#b" ct:size="1"> <rdf:li>One</rdf:li> <rdf:li>One</rdf:li> </rdf:Bag>
<eg:Set rdf:about="http://example.org/#b" ct:size="1"> <rdf:li>One</rdf:li> <rdf:li>Two</rdf:li> </eg:Set>
From a layering point of view, this treatment of containers is a nonmonotonic extension of RDFS. I.e. some entailments that are RDFS entailments are not container entailments, and vice-versa.
On the other hand c-entailment is monotonic. Adding premises never results in deletion of conclusions.
This seems to reflect that trying to account for the meaning of containers in M&S in exactly the same way as M&S accounts for other meanings is not satisfactory.
I believe that the ontology community has good used to some of
the advantages of
parseType="daml:collection".
Namely:
Hence, I think we need to deliver an
rdf:parseType="closed-bag"
or similar.
This could be identical in surface syntax to daml:collection
but generate
rdf:_type rdf:Bag triple;
<rdf:_1>
<rdf:_2>
... properties in place of the daml:List structure;
ct:size="n"
triple at the end of the bag.
For example:
<rdf:Description>
<eg:foo rdf:parseType="closed-bag>
<eg:bar />
<eg:baz />
</eg:foo>
</rdf:Description>
is shorthand for:
<rdf:Description>
<eg:foo rdf:parseType="closed-bag>
<rdf:Bag ct:size="2">
<rdf:li>
<eg:bar />
</rdf:li>
<rdf:li>
<eg:baz />
</rdf:li>
</rdf:Bag>
</eg:foo>
</rdf:Description>
I see substantial advantage in also permitting the very same construction on the typed-node construction (not just the property-element construction). This would permit lists of typed nodes directly inside a typed node. For example:
<rdf:Description rdf:parseType="closed-bag>
<eg:bar />
<eg:baz />
</rdf:Description>
Being shorthand for
<rdf:Description rdf:type="http:...#Bag" ct:size="2">
<rdf:li>
<eg:bar />
</rdf:li>
<rdf:li>
<eg:baz />
</rdf:li>
</rdf:Description>
The advantage is that then the striped syntax can be broken at any point with appropriate use of parsetype, making it more plausible that by a liberal sprinkling of parsetypes any XML document type definition can be turned into an appropriate RDF/XML subdialect.
This proposal puts container processing after schema processing. This reflects what I have heard on RDF Core. However, the earlier RDF work finished containers (in M&S)and did not finish schema (which has not yet got to REC). This suggests that the current recommendation puts container processing before schema processing. Since these two different layerings give different answers this is a non-trivial matter.
Moreover, the fact that there are syntactic rules in M&S for containers, suggest that the authors intended an early processing of containers, before schema processing, not after.
This is attractive because a version of this proposal which made the container processing into a syntactic transform, would have entirely monotonic semantics. (The rdf:_iii properties would no longer be put of the graph and would vanish in a way similar to rdf:li). That would not appear to be a rearticulation of M&S but a fairly significant change; that may be appropriate in RDF 2. Such a change is much more difficult (impossible?) if container processing happens after schema processing.
In the intended construction each of the constructed rdf:value
edges has one subject and one object.
This constraint could be made a strict requirement, changing the result of
this testcase.
Since GENSYM and IMEM as mapping from the graph syntax, it is necessary to have a graph to map from. With the choice of doing containers after schema, this constrains us to thinking of schema as a closure (which delivers the graph) rather than a set of constraints on an interpretation (which merely delivers an interpretation).
Introducing a node for each triple and relating the subject and object of the triple to that node is very reminiscient of reification. It might have been more elegant to use reification instead of a new mechanism.