Abstract
This specification defines the 2D Context for the HTML
canvas element.
Status of This document
This section describes the status of this document at the
time of its publication. Other documents may supersede this
document. A list of current W3C publications and the most recently
formally published revision of this technical report can be found in
the W3C technical reports index
at http://www.w3.org/TR/.
If you wish to make comments regarding this document in a manner
that is tracked by the W3C, please submit them via using our
public bug database. If you do not have an account then you can
enter feedback using this form:
If you cannot do this then you can also e-mail feedback to public-html-comments@w3.org
(subscribe,
archives),
and arrangements will be made to transpose the comments to our
public bug database.
Alternatively, you can e-mail feedback to whatwg@whatwg.org (subscribe,
archives).
The editor guarantees that all substantive feedback sent to this
list will receive a reply. However, such feedback is not considered
formal feedback for the W3C process.
All feedback is welcome.
The working groups maintains a
list of all bug reports that the editor has not yet tried to
address and a list of issues
for which the chairs have not yet declared a decision. The
editor also maintains a list
of all e-mails that he has not yet tried to address. These bugs,
issues, and e-mails apply to multiple HTML-related specifications,
not just this one.
Implementors should be aware that this specification is not
stable. Implementors who are not taking part in the
discussions are likely to find the specification changing out from
under them in incompatible ways. Vendors interested in
implementing this specification before it eventually reaches the
Candidate Recommendation stage should join the aforementioned
mailing lists and take part in the discussions.
The publication of this document by the W3C as a W3C Working
Draft does not imply that all of the participants in the W3C HTML
working group endorse the contents of the specification. Indeed, for
any section of the specification, one can usually find many members
of the working group or of the W3C as a whole who object strongly to
the current text, the existence of the section at all, or the idea
that the working group should even spend time discussing the concept
of that section.
The latest stable version of the editor's draft of this
specification is always available on the W3C CVS server and in the WHATWG Subversion
repository. The latest
editor's working copy (which may contain unfinished text in the
process of being prepared) contains the latest draft text of this
specification (amongst others). For more details, please see the WHATWG
FAQ.
There are various ways to follow the change history for the
HTML specifications:
- E-mail notifications of changes
- HTML-Diffs mailing list (diff-marked HTML versions for each change): http://lists.w3.org/Archives/Public/public-html-diffs/latest
- Commit-Watchers mailing list (complete source diffs): http://lists.whatwg.org/listinfo.cgi/commit-watchers-whatwg.org
- Real-time notifications of changes:
- Generated diff-marked HTML versions for each change: http://twitter.com/HTML5
- Browsable version-control record of all changes:
- CVSWeb interface with side-by-side diffs: http://dev.w3.org/cvsweb/html5/
- Annotated summary with unified diffs: http://html5.org/tools/web-apps-tracker
- Raw Subversion interface:
svn checkout http://svn.whatwg.org/webapps/
The W3C HTML Working
Group is the W3C working group responsible for this
specification's progress along the W3C Recommendation
track.
This specification is the 28 February 2011 Editor's Draft.
Work on this specification is also done at the WHATWG. The W3C HTML working group
actively pursues convergence with the WHATWG, as required by the W3C HTML working
group charter.
This specification is an extension to the HTML5 language. All
normative content in the HTML5 specification, unless specifically
overridden by this specification, is intended to be the basis for
this specification.
This document was produced by a group operating under the 5
February 2004 W3C Patent Policy. W3C maintains a public list of
any patent disclosures made in connection with the deliverables
of the group; that page also includes instructions for disclosing a
patent. An individual who has actual knowledge of a patent which the
individual believes contains Essential
Claim(s) must disclose the information in accordance with section
6 of the W3C Patent Policy.
Table of Contents
- 1 Conformance requirements
- 2 The canvas state
- 3 Transformations
- 4 Compositing
- 5 Colors and styles
- 6 Line styles
- 7 Shadows
- 8 Simple shapes (rectangles)
- 9 Complex shapes (paths)
<ZZZ>
- 10 Focus management
- 11 Caret and selection management
- 12 Text
- 13 Images
- 14 Pixel manipulation
- 15 Drawing model
- 16 Examples
</ZZZ>
- References
- Acknowledgements
This specification is an HTML specification. All the conformance
requirements, conformance classes, definitions, dependencies,
terminology, and typographical conventions described in the core
HTML5 specification apply to this specification. [HTML5]
Interfaces are defined in terms of Web IDL. [WEBIDL]
This specification defines the 2d context type, whose
API is implemented using the CanvasRenderingContext2D
interface.
When the getContext()
method of a canvas element is to return a new object for the contextId 2d, the user agent must return a
new CanvasRenderingContext2D object. Any additional
arguments are ignored.
The 2D context represents a flat Cartesian surface whose origin
(0,0) is at the top left corner, with the coordinate space having
x values increasing when going right, and y values increasing when going down.
interface CanvasRenderingContext2D {
// back-reference to the canvas
readonly attribute HTMLCanvasElement canvas;
// state
void save(); // push state on state stack
void restore(); // pop state stack and restore state
// transformations (default transform is the identity matrix)
void scale(in double x, in double y);
void rotate(in double angle);
void translate(in double x, in double y);
void transform(in double a, in double b, in double c, in double d, in double e, in double f);
void setTransform(in double a, in double b, in double c, in double d, in double e, in double f);
// compositing
attribute double globalAlpha; // (default 1.0)
attribute DOMString globalCompositeOperation; // (default source-over)
// colors and styles
attribute any strokeStyle; // (default black)
attribute any fillStyle; // (default black)
CanvasGradient createLinearGradient(in double x0, in double y0, in double x1, in double y1);
CanvasGradient createRadialGradient(in double x0, in double y0, in double r0, in double x1, in double y1, in double r1);
CanvasPattern createPattern(in HTMLImageElement image, in DOMString repetition);
CanvasPattern createPattern(in HTMLCanvasElement image, in DOMString repetition);
CanvasPattern createPattern(in HTMLVideoElement image, in DOMString repetition);
// line caps/joins
attribute double lineWidth; // (default 1)
attribute DOMString lineCap; // "butt", "round", "square" (default "butt")
attribute DOMString lineJoin; // "round", "bevel", "miter" (default "miter")
attribute double miterLimit; // (default 10)
// shadows
attribute double shadowOffsetX; // (default 0)
attribute double shadowOffsetY; // (default 0)
attribute double shadowBlur; // (default 0)
attribute DOMString shadowColor; // (default transparent black)
// rects
void clearRect(in double x, in double y, in double w, in double h);
void fillRect(in double x, in double y, in double w, in double h);
void strokeRect(in double x, in double y, in double w, in double h);
// path API
void beginPath();
void closePath();
void moveTo(in double x, in double y);
void lineTo(in double x, in double y);
void quadraticCurveTo(in double cpx, in double cpy, in double x, in double y);
void bezierCurveTo(in double cp1x, in double cp1y, in double cp2x, in double cp2y, in double x, in double y);
void arcTo(in double x1, in double y1, in double x2, in double y2, in double radius);
void rect(in double x, in double y, in double w, in double h);
void arc(in double x, in double y, in double radius, in double startAngle, in double endAngle, in optional boolean anticlockwise);
void fill();
void stroke();
void clip();
boolean isPointInPath(in double x, in double y);
<ZZZ>
// Focus management
boolean drawFocusRing(in Element element, in optional boolean canDrawCustom);
// Caret and selection management
long caretBlinkRate();
boolean setCaretSelectionRect(in Element element, in double x, in double y, in double w, in double h);
</ZZZ>
// text
attribute DOMString font; // (default 10px sans-serif)
attribute DOMString textAlign; // "start", "end", "left", "right", "center" (default: "start")
attribute DOMString textBaseline; // "top", "hanging", "middle", "alphabetic", "ideographic", "bottom" (default: "alphabetic")
void fillText(in DOMString text, in double x, in double y, in optional double maxWidth);
void strokeText(in DOMString text, in double x, in double y, in optional double maxWidth);
TextMetrics measureText(in DOMString text);
// drawing images
void drawImage(in HTMLImageElement image, in double dx, in double dy, in optional double dw, in double dh);
void drawImage(in HTMLImageElement image, in double sx, in double sy, in double sw, in double sh, in double dx, in double dy, in double dw, in double dh);
void drawImage(in HTMLCanvasElement image, in double dx, in double dy, in optional double dw, in double dh);
void drawImage(in HTMLCanvasElement image, in double sx, in double sy, in double sw, in double sh, in double dx, in double dy, in double dw, in double dh);
void drawImage(in HTMLVideoElement image, in double dx, in double dy, in optional double dw, in double dh);
void drawImage(in HTMLVideoElement image, in double sx, in double sy, in double sw, in double sh, in double dx, in double dy, in double dw, in double dh);
// pixel manipulation
ImageData createImageData(in double sw, in double sh);
ImageData createImageData(in ImageData imagedata);
ImageData getImageData(in double sx, in double sy, in double sw, in double sh);
void putImageData(in ImageData imagedata, in double dx, in double dy, in optional double dirtyX, in double dirtyY, in double dirtyWidth, in double dirtyHeight);
};
interface CanvasGradient {
// opaque object
void addColorStop(in double offset, in DOMString color);
};
interface CanvasPattern {
// opaque object
};
interface TextMetrics {
readonly attribute double width;
};
interface ImageData {
readonly attribute unsigned long width;
readonly attribute unsigned long height;
readonly attribute CanvasPixelArray data;
};
interface CanvasPixelArray {
readonly attribute unsigned long length;
getter octet (in unsigned long index);
setter void (in unsigned long index, in octet value);
};- context .
canvas
-
Returns the canvas element.
The canvas
attribute must return the canvas element that the
context paints on.
Except where otherwise specified, for the 2D context interface,
any method call with a numeric argument whose value is infinite or a
NaN value must be ignored.
Whenever the CSS value currentColor is used
as a color in this API, the "computed value of the 'color' property"
for the purposes of determining the computed value of the currentColor keyword is the computed value of the
'color' property on the element in question at the time that the
color is specified (e.g. when the appropriate attribute is set, or
when the method is called; not when the color is rendered or
otherwise used). If the computed value of the 'color' property is
undefined for a particular case (e.g. because the element is not
in a Document), then the "computed value
of the 'color' property" for the purposes of determining the
computed value of the currentColor keyword is
fully opaque black. [CSSCOLOR]
In the case of addColorStop() on
CanvasGradient, the "computed value of the 'color'
property" for the purposes of determining the computed value of the
currentColor keyword is always fully opaque
black (there is no associated element). [CSSCOLOR]
This is because CanvasGradient objects
are canvas-neutral — a
CanvasGradient object created by one
canvas can be used by another, and there is therefore
no way to know which is the "element in question" at the time that
the color is specified.
2 The canvas state
Each context maintains a stack of drawing states. Drawing states consist of:
- The current transformation matrix.
- The current clipping region.
- The current values of the following attributes:
strokeStyle, fillStyle, globalAlpha, lineWidth, lineCap, lineJoin, miterLimit, shadowOffsetX, shadowOffsetY, shadowBlur, shadowColor, globalCompositeOperation, font, textAlign, textBaseline.
The current path and the current bitmap are not part
of the drawing state. The current path is persistent, and can only
be reset using the beginPath() method. The
current bitmap is a property of the canvas, not the context.
- context .
save()
-
Pushes the current state onto the stack.
- context .
restore()
-
Pops the top state on the stack, restoring the context to that state.
The save()
method must push a copy of the current drawing state onto the
drawing state stack.
The restore() method
must pop the top entry in the drawing state stack, and reset the
drawing state it describes. If there is no saved state, the method
must do nothing.
The transformation matrix is applied to coordinates when creating
shapes and paths.
When the context is created, the transformation matrix must
initially be the identity transform. It may then be adjusted using
the transformation methods.
The transformations must be performed in reverse order. For
instance, if a scale transformation that doubles the width is
applied, followed by a rotation transformation that rotates drawing
operations by a quarter turn, and a rectangle twice as wide as it is
tall is then drawn on the canvas, the actual result will be a
square.
- context .
scale(x, y)
-
Changes the transformation matrix to apply a scaling transformation with the given characteristics.
- context .
rotate(angle)
-
Changes the transformation matrix to apply a rotation transformation with the given characteristics. The angle is in radians.
- context .
translate(x, y)
-
Changes the transformation matrix to apply a translation transformation with the given characteristics.
- context .
transform(a, b, c, d, e, f)
-
Changes the transformation matrix to apply the matrix given by the arguments as described below.
- context .
setTransform(a, b, c, d, e, f)
-
Changes the transformation matrix to the matrix given by the arguments as described below.
The scale(x, y) method must
add the scaling transformation described by the arguments to the
transformation matrix. The x argument represents
the scale factor in the horizontal direction and the y argument represents the scale factor in the
vertical direction. The factors are multiples.
The rotate(angle) method must add the rotation
transformation described by the argument to the transformation
matrix. The angle argument represents a
clockwise rotation angle expressed in radians.
The translate(x, y) method must
add the translation transformation described by the arguments to the
transformation matrix. The x argument represents
the translation distance in the horizontal direction and the y argument represents the translation distance in the
vertical direction. The arguments are in coordinate space units.
The transform(a, b, c, d, e, f) method must replace the current
transformation matrix with the result of multiplying the current
transformation matrix with the matrix described by:
The arguments a, b, c, d, e, and f are sometimes called
m11, m12, m21, m22, dx,
and dy or m11, m21, m12, m22, dx, and dy. Care should be taken in particular with the order
of the second and third arguments (b and c) as their order varies from API to API and APIs
sometimes use the notation m12/m21 and sometimes m21/m12 for those positions.
The setTransform(a, b, c, d, e,
f) method must reset the current
transform to the identity matrix, and then invoke the transform(a, b, c, d, e,
f) method with the same arguments.
4 Compositing
- context .
globalAlpha [ = value ]
-
Returns the current alpha value applied to rendering operations.
Can be set, to change the alpha value. Values outside of the
range 0.0 .. 1.0 are ignored.
- context .
globalCompositeOperation [ = value ]
-
Returns the current composition operation, from the list below.
Can be set, to change the composition operation. Unknown values
are ignored.
All drawing operations are affected by the global compositing
attributes, globalAlpha and globalCompositeOperation.
The globalAlpha
attribute gives an alpha value that is applied to shapes and images
before they are composited onto the canvas. The value must be in the
range from 0.0 (fully transparent) to 1.0 (no additional
transparency). If an attempt is made to set the attribute to a value
outside this range, including Infinity and Not-a-Number (NaN)
values, the attribute must retain its previous value. When the
context is created, the globalAlpha attribute must
initially have the value 1.0.
The globalCompositeOperation
attribute sets how shapes and images are drawn onto the existing
bitmap, once they have had globalAlpha and the
current transformation matrix applied. It must be set to a value
from the following list. In the descriptions below, the source
image, A, is the shape or image being rendered,
and the destination image, B, is the current
state of the bitmap.
source-atop- A atop B. Display the
source image wherever both images are opaque. Display the
destination image wherever the destination image is opaque but the
source image is transparent. Display transparency elsewhere.
source-in- A in B. Display the
source image wherever both the source image and destination image
are opaque. Display transparency elsewhere.
source-out- A out B. Display the
source image wherever the source image is opaque and the
destination image is transparent. Display transparency
elsewhere.
source-over (default)- A over B. Display the
source image wherever the source image is opaque. Display the
destination image elsewhere.
destination-atop- B atop A. Same as
source-atop but using the
destination image instead of the source image and vice versa.
destination-in- B in A. Same as
source-in but using the destination
image instead of the source image and vice versa.
destination-out- B out A. Same as
source-out but using the destination
image instead of the source image and vice versa.
destination-over- B over A. Same as
source-over but using the
destination image instead of the source image and vice versa.
lighter- A plus B. Display the
sum of the source image and destination image, with color values
approaching 255 (100%) as a limit.
copy- A (B is
ignored). Display the source image instead of the destination
image.
xor- A xor B. Exclusive OR
of the source image and destination image.
vendorName-operationName- Vendor-specific extensions to the list of
composition operators should use this syntax.
The operators in the above list must be treated as described by
the Porter-Duff operator given at the start of their description
(e.g. A over B). They are to
be applied as part of the drawing model, at which point the
clipping region is also applied. (Without a clipping
region, these operators act on the whole bitmap with every
operation.) [PORTERDUFF]
These values are all case-sensitive — they must be used
exactly as shown. User agents must not recognize values that are not
a case-sensitive match for one of the values given
above.
On setting, if the user agent does not recognize the specified
value, it must be ignored, leaving the value of globalCompositeOperation
unaffected.
When the context is created, the globalCompositeOperation
attribute must initially have the value
source-over.
5 Colors and styles
- context .
strokeStyle [ = value ]
-
Returns the current style used for stroking shapes.
Can be set, to change the stroke style.
The style can be either a string containing a CSS color, or a
CanvasGradient or CanvasPattern
object. Invalid values are ignored.
- context .
fillStyle [ = value ]
-
Returns the current style used for filling shapes.
Can be set, to change the fill style.
The style can be either a string containing a CSS color, or a
CanvasGradient or CanvasPattern
object. Invalid values are ignored.
The strokeStyle
attribute represents the color or style to use for the lines around
shapes, and the fillStyle
attribute represents the color or style to use inside the
shapes.
Both attributes can be either strings,
CanvasGradients, or CanvasPatterns. On
setting, strings must be parsed as CSS <color> values and the color
assigned, and CanvasGradient and
CanvasPattern objects must be assigned themselves. [CSSCOLOR] If the value is a string but
cannot be parsed as a CSS <color> value, or is
neither a string, a CanvasGradient, nor a
CanvasPattern, then it must be ignored, and the
attribute must retain its previous value.
When set to a CanvasPattern or
CanvasGradient object, the assignment is
live, meaning that changes made to the object after the
assignment do affect subsequent stroking or filling of shapes.
On getting, if the value is a color, then the serialization of the color
must be returned. Otherwise, if it is not a color but a
CanvasGradient or CanvasPattern, then the
respective object must be returned. (Such objects are opaque and
therefore only useful for assigning to other attributes or for
comparison to other gradients or patterns.)
The serialization of a color for a color value is a
string, computed as follows: if it has alpha equal to 1.0, then the
string is a lowercase six-digit hex value, prefixed with a "#"
character (U+0023 NUMBER SIGN), with the first two digits
representing the red component, the next two digits representing the
green component, and the last two digits representing the blue
component, the digits being in the range 0-9 a-f (U+0030 to U+0039
and U+0061 to U+0066). Otherwise, the color value has alpha less
than 1.0, and the string is the color value in the CSS rgba() functional-notation format: the literal
string rgba (U+0072 U+0067 U+0062 U+0061)
followed by a U+0028 LEFT PARENTHESIS, a base-ten integer in the
range 0-255 representing the red component (using digits 0-9, U+0030
to U+0039, in the shortest form possible), a literal U+002C COMMA
and U+0020 SPACE, an integer for the green component, a comma and a
space, an integer for the blue component, another comma and space, a
U+0030 DIGIT ZERO, if the alpha value is greater than zero then a
U+002E FULL STOP (representing the decimal point), if the alpha
value is greater than zero then one or more digits in the range 0-9
(U+0030 to U+0039) representing the fractional part of the alpha
value, and finally a U+0029 RIGHT PARENTHESIS.
When the context is created, the strokeStyle and fillStyle attributes must
initially have the string value #000000.
There are two types of gradients, linear gradients and radial
gradients, both represented by objects implementing the opaque
CanvasGradient interface.
Once a gradient has been created (see below),
stops are placed along it to define how the colors are distributed
along the gradient. The color of the gradient at
each stop is the color specified for that stop. Between each such
stop, the colors and the alpha component must be linearly
interpolated over the RGBA space without premultiplying the alpha
value to find the color to use at that offset. Before the first
stop, the color must be the color of the first stop. After the last
stop, the color must be the color of the last stop. When there are
no stops, the gradient is transparent black.
- gradient .
addColorStop(offset, color)
-
Adds a color stop with the given color to the gradient at the
given offset. 0.0 is the offset at one end of the gradient, 1.0 is
the offset at the other end.
Throws an INDEX_SIZE_ERR exception if the offset
is out of range. Throws a SYNTAX_ERR exception if the
color cannot be parsed.
- gradient = context .
createLinearGradient(x0, y0, x1, y1)
-
Returns a CanvasGradient object that represents a
linear gradient that paints along the line given by the
coordinates represented by the arguments.
If any of the arguments are not finite numbers, throws a
NOT_SUPPORTED_ERR exception.
- gradient = context .
createRadialGradient(x0, y0, r0, x1, y1, r1)
-
Returns a CanvasGradient object that represents a
radial gradient that paints along the cone given by the circles
represented by the arguments.
If any of the arguments are not finite numbers, throws a
NOT_SUPPORTED_ERR exception. If either of the radii
are negative, throws an INDEX_SIZE_ERR exception.
The addColorStop(offset, color)
method on the CanvasGradient interface adds a new stop
to a gradient. If the offset is less than 0,
greater than 1, infinite, or NaN, then an
INDEX_SIZE_ERR exception must be raised. If the color cannot be parsed as a CSS <color>
value, then a SYNTAX_ERR exception must be
raised. Otherwise, the gradient must have a new stop placed, at
offset offset relative to the whole gradient,
and with the color obtained by parsing color as
a CSS <color> value. If multiple stops are added at the same
offset on a gradient, they must be placed in the order added, with
the first one closest to the start of the gradient, and each
subsequent one infinitesimally further along towards the end point
(in effect causing all but the first and last stop added at each
point to be ignored).
The createLinearGradient(x0, y0, x1,
y1) method takes four arguments
that represent the start point (x0, y0) and end point (x1, y1) of the gradient. If any of the arguments to createLinearGradient()
are infinite or NaN, the method must raise a
NOT_SUPPORTED_ERR exception. Otherwise, the method must
return a linear CanvasGradient initialized with the
specified line.
Linear gradients must be rendered such that all points on a line
perpendicular to the line that crosses the start and end points have
the color at the point where those two lines cross (with the colors
coming from the interpolation and
extrapolation described above). The points in the linear
gradient must be transformed as described by the current transformation
matrix when rendering.
If x0 = x1 and y0 = y1, then
the linear gradient must paint nothing.
The createRadialGradient(x0, y0, r0,
x1, y1, r1) method takes six arguments, the
first three representing the start circle with origin (x0, y0) and radius r0, and the last three representing the end circle
with origin (x1, y1) and
radius r1. The values are in coordinate space
units. If any of the arguments are infinite or NaN, a
NOT_SUPPORTED_ERR exception must be raised. If either
of r0 or r1 are negative, an
INDEX_SIZE_ERR exception must be raised. Otherwise,
the method must return a radial CanvasGradient
initialized with the two specified circles.
Radial gradients must be rendered by following these steps:
If x0 = x1 and y0 = y1 and r0 = r1, then the radial gradient must
paint nothing. Abort these steps.
-
Let x(ω) = (x1-x0)ω + x0
Let y(ω) = (y1-y0)ω + y0
Let r(ω) = (r1-r0)ω + r0
Let the color at ω be the color at
that position on the gradient (with the colors coming from the interpolation and extrapolation
described above).
For all values of ω where r(ω) > 0,
starting with the value of ω nearest to
positive infinity and ending with the value of ω nearest to negative infinity, draw the
circumference of the circle with radius r(ω) at position (x(ω), y(ω)), with the color at ω, but only painting on the parts of the
canvas that have not yet been painted on by earlier circles in this
step for this rendering of the gradient.
This effectively creates a cone, touched by the two
circles defined in the creation of the gradient, with the part of
the cone before the start circle (0.0) using the color of the first
offset, the part of the cone after the end circle (1.0) using the
color of the last offset, and areas outside the cone untouched by
the gradient (transparent black).
The points in the radial gradient must be transformed as
described by the current
transformation matrix when rendering.
Gradients must be painted only where the relevant stroking or
filling effects requires that they be drawn.
Patterns are represented by objects implementing the opaque
CanvasPattern interface.
- pattern = context .
createPattern(image, repetition)
-
Returns a CanvasPattern object that uses the given image
and repeats in the direction(s) given by the repetition argument.
The allowed values for repetition are repeat (both directions), repeat-x (horizontal only), repeat-y (vertical only), and no-repeat (neither). If the repetition argument is empty or null, the value
repeat is used.
If the first argument isn't an img,
canvas, or video element, throws a
TYPE_MISMATCH_ERR exception. If the image has no
image data, throws an INVALID_STATE_ERR exception. If
the second argument isn't one of the allowed values, throws a
SYNTAX_ERR exception. If the image isn't yet fully
decoded, then the method returns null.
To create objects of this type, the createPattern(image, repetition)
method is used. The first argument gives the image to use as the
pattern (either an HTMLImageElement,
HTMLCanvasElement, or HTMLVideoElement
object). Modifying this image after calling the createPattern() method
must not affect the pattern. The second argument must be a string
with one of the following values: repeat,
repeat-x, repeat-y,
no-repeat. If the empty string or null is
specified, repeat must be assumed. If an
unrecognized value is given, then the user agent must raise a
SYNTAX_ERR exception. User agents must recognize the
four values described above exactly (e.g. they must not do case
folding). Except as specified below, the method must return a
CanvasPattern object suitably initialized.
The image argument is an instance of either
HTMLImageElement, HTMLCanvasElement, or
HTMLVideoElement. If the image is
null, the implementation must raise a TYPE_MISMATCH_ERR
exception.
If the image argument is an
HTMLImageElement object that is not fully decodable, or if the image argument is an HTMLVideoElement
object whose readyState
attribute is either HAVE_NOTHING or HAVE_METADATA, then the
implementation must return null.
If the image argument is an
HTMLCanvasElement object with either a horizontal
dimension or a vertical dimension equal to zero, then the
implementation must raise an INVALID_STATE_ERR
exception.
Patterns must be painted so that the top left of the first image
is anchored at the origin of the coordinate space, and images are
then repeated horizontally to the left and right (if the
repeat-x string was specified) or vertically up and
down (if the repeat-y string was specified) or in all
four directions all over the canvas (if the repeat
string was specified). The images are not scaled by this process;
one CSS pixel of the image must be painted on one coordinate space
unit. Of course, patterns must actually be painted only where the
stroking or filling effect requires that they be drawn, and are
affected by the current transformation matrix.
If the original image data is a bitmap image, the value painted
at a point in the area of the repetitions is computed by filtering
the original image data. The user agent may use any filtering
algorithm (for example bilinear interpolation or nearest-neighbor).
When the filtering algorithm requires a pixel value from outside the
original image data, it must instead use the value from wrapping the
pixel's coordinates to the original image's dimensions. (That is,
the filter uses 'repeat' behavior, regardless of the value of
repetition.)
When the createPattern() method
is passed an animated image as its image
argument, the user agent must use the poster frame of the animation,
or, if there is no poster frame, the first frame of the
animation.
When the image argument is an
HTMLVideoElement, then the frame at the current
playback position must be used as the source image, and the
source image's dimensions must be the intrinsic width and
intrinsic height
of the media resource (i.e. after any aspect-ratio
correction has been applied).
6 Line styles
- context .
lineWidth [ = value ]
-
Returns the current line width.
Can be set, to change the line width. Values that are not
finite values greater than zero are ignored.
- context .
lineCap [ = value ]
-
Returns the current line cap style.
Can be set, to change the line cap style.
The possible line cap styles are butt,
round, and square. Other values are
ignored.
- context .
lineJoin [ = value ]
-
Returns the current line join style.
Can be set, to change the line join style.
The possible line join styles are bevel,
round, and miter. Other values are
ignored.
- context .
miterLimit [ = value ]
-
Returns the current miter limit ratio.
Can be set, to change the miter limit ratio. Values that are
not finite values greater than zero are ignored.
The lineWidth
attribute gives the width of lines, in coordinate space units. On
getting, it must return the current value. On setting, zero,
negative, infinite, and NaN values must be ignored, leaving the
value unchanged; other values must change the current value to the
new value.
When the context is created, the lineWidth attribute must
initially have the value 1.0.
The lineCap attribute
defines the type of endings that UAs will place on the end of
lines. The three valid values are butt,
round, and square. The butt
value means that the end of each line has a flat edge perpendicular
to the direction of the line (and that no additional line cap is
added). The round value means that a semi-circle with
the diameter equal to the width of the line must then be added on to
the end of the line. The square value means that a
rectangle with the length of the line width and the width of half
the line width, placed flat against the edge perpendicular to the
direction of the line, must be added at the end of each line.
On getting, it must return the current value. On setting, if the
new value is one of the literal strings butt,
round, and square, then the current value
must be changed to the new value; other values must ignored, leaving
the value unchanged.
When the context is created, the lineCap attribute must
initially have the value butt.
The lineJoin
attribute defines the type of corners that UAs will place where two
lines meet. The three valid values are bevel,
round, and miter.
On getting, it must return the current value. On setting, if the
new value is one of the literal strings bevel,
round, and miter, then the current value
must be changed to the new value; other values must be ignored,
leaving the value unchanged.
When the context is created, the lineJoin attribute must
initially have the value miter.
A join exists at any point in a subpath shared by two consecutive
lines. When a subpath is closed, then a join also exists at its
first point (equivalent to its last point) connecting the first and
last lines in the subpath.
In addition to the point where the join occurs, two additional
points are relevant to each join, one for each line: the two corners
found half the line width away from the join point, one
perpendicular to each line, each on the side furthest from the other
line.
A filled triangle connecting these two opposite corners with a
straight line, with the third point of the triangle being the join
point, must be rendered at all joins. The lineJoin attribute controls
whether anything else is rendered. The three aforementioned values
have the following meanings:
The bevel value means that this is all that is
rendered at joins.
The round value means that a filled arc connecting
the two aforementioned corners of the join, abutting (and not
overlapping) the aforementioned triangle, with the diameter equal to
the line width and the origin at the point of the join, must be
rendered at joins.
The miter value means that a second filled triangle
must (if it can given the miter length) be rendered at the join,
with one line being the line between the two aforementioned corners,
abutting the first triangle, and the other two being continuations of
the outside edges of the two joining lines, as long as required to
intersect without going over the miter length.
The miter length is the distance from the point where the join
occurs to the intersection of the line edges on the outside of the
join. The miter limit ratio is the maximum allowed ratio of the
miter length to half the line width. If the miter length would cause
the miter limit ratio to be exceeded, this second triangle must not
be rendered.
The miter limit ratio can be explicitly set using the miterLimit
attribute. On getting, it must return the current value. On setting,
zero, negative, infinite, and NaN values must be ignored, leaving
the value unchanged; other values must change the current value to
the new value.
When the context is created, the miterLimit attribute must
initially have the value 10.0.
7 Shadows
All drawing operations are affected by the four global shadow
attributes.
- context .
shadowColor [ = value ]
-
Returns the current shadow color.
Can be set, to change the shadow color. Values that cannot be parsed as CSS colors are ignored.
- context .
shadowOffsetX [ = value ]
- context .
shadowOffsetY [ = value ]
-
Returns the current shadow offset.
Can be set, to change the shadow offset. Values that are not finite numbers are ignored.
- context .
shadowBlur [ = value ]
-
Returns the current level of blur applied to shadows.
Can be set, to change the blur level. Values that are not finite numbers greater than or equal to zero are ignored.
The shadowColor
attribute sets the color of the shadow.
When the context is created, the shadowColor attribute
initially must be fully-transparent black.
On getting, the serialization of the color must be returned.
On setting, the new value must be parsed as a CSS
<color> value and the color assigned. If the value
cannot be parsed as a CSS <color> value then it must be
ignored, and the attribute must retain its previous value. [CSSCOLOR]
The shadowOffsetX
and shadowOffsetY
attributes specify the distance that the shadow will be offset in
the positive horizontal and positive vertical distance
respectively. Their values are in coordinate space units. They are
not affected by the current transformation matrix.
When the context is created, the shadow offset attributes must
initially have the value 0.
On getting, they must return their current value. On setting, the
attribute being set must be set to the new value, except if the
value is infinite or NaN, in which case the new value must be
ignored.
The shadowBlur
attribute specifies the level of the blurring effect. (The units do
not map to coordinate space units, and are not affected by the
current transformation matrix.)
When the context is created, the shadowBlur attribute must
initially have the value 0.
On getting, the attribute must return its current value. On
setting the attribute must be set to the new value, except if the
value is negative, infinite or NaN, in which case the new value must
be ignored.
Shadows are only drawn
if the opacity component of the alpha component of the color
of shadowColor is
non-zero and either the shadowBlur is non-zero, or
the shadowOffsetX
is non-zero, or the shadowOffsetY is
non-zero.
When shadows are drawn, they must be rendered as follows:
-
Let A be an infinite transparent black
bitmap on which the source image for which a shadow is being
created has been rendered.
-
Let B be an infinite transparent black
bitmap, with a coordinate space and an origin identical to A.
-
Copy the alpha channel of A to B, offset by shadowOffsetX in the
positive x direction, and shadowOffsetY in the
positive y direction.
-
If shadowBlur is greater than
0:
-
Let σ be half the value of
shadowBlur.
-
Perform a 2D Gaussian Blur on B,
using σ as the standard deviation.
User agents may limit values of σ to
an implementation-specific maximum value to avoid exceeding
hardware limitations during the Gaussian blur operation.
-
Set the red, green, and blue components of every pixel in
B to the red, green, and blue components
(respectively) of the color of shadowColor.
-
Multiply the alpha component of every pixel in B by the alpha component of the color of shadowColor.
-
The shadow is in the bitmap B, and is
rendered as part of the drawing model described below.
If the current composition operation is copy, shadows effectively won't render
(since the shape will overwrite the shadow).
8 Simple shapes (rectangles)
There are three methods that immediately draw rectangles to the
bitmap. They each take four arguments; the first two give the x and y coordinates of the top
left of the rectangle, and the second two give the width w and height h of the rectangle,
respectively.
The current
transformation matrix must be applied to the following four
coordinates, which form the path that must then be closed to get the
specified rectangle: (x, y), (x+w, y),
(x+w,
y+h),
(x, y+h).
Shapes are painted without affecting the current path, and are
subject to the clipping region,
and, with the exception of clearRect(), also shadow effects, global alpha, and global composition
operators.
- context .
clearRect(x, y, w, h)
-
Clears all pixels on the canvas in the given rectangle to transparent black.
- context .
fillRect(x, y, w, h)
-
Paints the given rectangle onto the canvas, using the current fill style.
- context .
strokeRect(x, y, w, h)
-
Paints the box that outlines the given rectangle onto the canvas, using the current stroke style.
The clearRect(x, y, w, h) method must clear the pixels in the
specified rectangle that also intersect the current clipping region
to a fully transparent black, erasing any previous image. If either
height or width are zero, this method has no effect.
The fillRect(x, y, w, h) method must paint the specified
rectangular area using the fillStyle. If either height
or width are zero, this method has no effect.
The strokeRect(x, y, w, h) method must stroke the specified
rectangle's path using the strokeStyle, lineWidth, lineJoin, and (if
appropriate) miterLimit attributes. If
both height and width are zero, this method has no effect, since
there is no path to stroke (it's a point). If only one of the two is
zero, then the method will draw a line instead (the path for the
outline is just a straight line along the non-zero dimension).
9 Complex shapes (paths)
The context always has a current path. There is only one current
path, it is not part of the drawing state.
A path has a list of zero or more subpaths. Each
subpath consists of a list of one or more points, connected by
straight or curved lines, and a flag indicating whether the subpath
is closed or not. A closed subpath is one where the last point of
the subpath is connected to the first point of the subpath by a
straight line. Subpaths with fewer than two points are ignored when
painting the path.
- context .
beginPath()
-
Resets the current path.
- context .
moveTo(x, y)
-
Creates a new subpath with the given point.
- context .
closePath()
-
Marks the current subpath as closed, and starts a new subpath with a point the same as the start and end of the newly closed subpath.
- context .
lineTo(x, y)
-
Adds the given point to the current subpath, connected to the previous one by a straight line.
- context .
quadraticCurveTo(cpx, cpy, x, y)
-
Adds the given point to the current subpath, connected to the previous one by a quadratic Bézier curve with the given control point.
- context .
bezierCurveTo(cp1x, cp1y, cp2x, cp2y, x, y)
-
Adds the given point to the current subpath, connected to the previous one by a cubic Bézier curve with the given control points.
- context .
arcTo(x1, y1, x2, y2, radius)
-
Adds an arc with the given control points and radius to the
current subpath, connected to the previous point by a straight
line.
Throws an INDEX_SIZE_ERR exception if the given
radius is negative.
- context .
arc(x, y, radius, startAngle, endAngle [, anticlockwise ] )
-
Adds points to the subpath such that the arc described by the
circumference of the circle described by the arguments, starting
at the given start angle and ending at the given end angle, going
in the given direction (defaulting to clockwise), is added to the
path, connected to the previous point by a straight line.
Throws an INDEX_SIZE_ERR exception if the given
radius is negative.
- context .
rect(x, y, w, h)
-
Adds a new closed subpath to the path, representing the given rectangle.
- context .
fill()
-
Fills the subpaths with the current fill style.
- context .
stroke()
-
Strokes the subpaths with the current stroke style.
- context .
clip()
-
Further constrains the clipping region to the given path.
- context .
isPointInPath(x, y)
-
Returns true if the given point is in the current path.
Initially, the context's path must have zero subpaths.
The points and lines added to the path by these methods must be
transformed according to the current transformation
matrix as they are added.
The beginPath()
method must empty the list of subpaths so that the context once
again has zero subpaths.
The moveTo(x, y) method must
create a new subpath with the specified point as its first (and
only) point.
When the user agent is to ensure there is a subpath
for a coordinate (x, y), the
user agent must check to see if the context has any subpaths, and if
it does not, then the user agent must create a new subpath with the
point (x, y) as its first
(and only) point, as if the moveTo() method had been
called.
The closePath()
method must do nothing if the context has no subpaths. Otherwise, it
must mark the last subpath as closed, create a new subpath whose
first point is the same as the previous subpath's first point, and
finally add this new subpath to the path.
If the last subpath had more than one point in its
list of points, then this is equivalent to adding a straight line
connecting the last point back to the first point, thus "closing"
the shape, and then repeating the last (possibly implied) moveTo() call.
New points and the lines connecting them are added to subpaths
using the methods described below. In all cases, the methods only
modify the last subpath in the context's paths.
The lineTo(x, y) method must
ensure there is a subpath for (x, y) if the context has
no subpaths. Otherwise, it must connect the last point in the
subpath to the given point (x, y) using a straight line, and must then add the given
point (x, y) to the
subpath.
The quadraticCurveTo(cpx, cpy, x,
y) method must ensure there
is a subpath for (cpx,
cpy), and then must connect the last
point in the subpath to the given point (x, y) using a quadratic Bézier curve with control
point (cpx, cpy), and must
then add the given point (x, y) to the subpath. [BEZIER]
The bezierCurveTo(cp1x, cp1y, cp2x, cp2y, x, y) method must
ensure there is a subpath for (cp1x, cp1y), and then must
connect the last point in the subpath to the given point (x, y) using a cubic Bézier
curve with control points (cp1x, cp1y) and (cp2x, cp2y). Then, it must add the point (x, y) to the subpath. [BEZIER]
The arcTo(x1, y1, x2,
y2, radius)
method must first ensure there is a subpath for (x1, y1). Then, the behavior depends on the
arguments and the last point in the subpath, as described below.
Negative values for radius must cause the
implementation to raise an INDEX_SIZE_ERR
exception.
Let the point (x0, y0) be
the last point in the subpath.
If the point (x0, y0) is
equal to the point (x1, y1),
or if the point (x1, y1) is
equal to the point (x2, y2),
or if the radius radius is zero, then the method
must add the point (x1, y1)
to the subpath, and connect that point to the previous point (x0, y0) by a straight line.
Otherwise, if the points (x0, y0), (x1, y1), and (x2, y2) all lie on a single straight line, then the
method must add the point (x1, y1) to the subpath, and connect that point to the
previous point (x0, y0) by a
straight line.
Otherwise, let The Arc be the shortest arc
given by circumference of the circle that has radius radius, and that has one point tangent to the
half-infinite line that crosses the point (x0,
y0) and ends at the point (x1, y1), and that has a different
point tangent to the half-infinite line that ends at the point (x1, y1) and crosses the point
(x2, y2). The points at
which this circle touches these two lines are called the start and
end tangent points respectively. The method must connect the point
(x0, y0) to the start
tangent point by a straight line, adding the start tangent point to
the subpath, and then must connect the start tangent point to the
end tangent point by The Arc, adding the end
tangent point to the subpath.
The arc(x, y, radius,
startAngle, endAngle, anticlockwise) method draws an arc. If
the context has any subpaths, then the method must add a straight
line from the last point in the subpath to the start point of the
arc. In any case, it must draw the arc between the start point of
the arc and the end point of the arc, and add the start and end
points of the arc to the subpath. The arc and its start and end
points are defined as follows:
Consider a circle that has its origin at (x,
y) and that has radius radius. The points at startAngle
and endAngle along this circle's circumference,
measured in radians clockwise from the positive x-axis, are the
start and end points respectively.
If the anticlockwise argument is omitted or
false and endAngle-startAngle is equal to or greater than 2π, or, if the anticlockwise
argument is true and startAngle-endAngle is
equal to or greater than 2π, then the arc
is the whole circumference of this circle.
Otherwise, the arc is the path along the circumference of this
circle from the start point to the end point, going anti-clockwise
if the anticlockwise argument is true, and
clockwise otherwise. Since the points are on the circle, as opposed
to being simply angles from zero, the arc can never cover an angle
greater than 2π radians. If the two points are the
same, or if the radius is zero, then the arc is defined as being of
zero length in both directions.
Negative values for radius must cause the
implementation to raise an INDEX_SIZE_ERR
exception.
The rect(x, y, w, h) method must create a new subpath
containing just the four points (x, y), (x+w,
y), (x+w, y+h),
(x, y+h), with those four points connected by straight
lines, and must then mark the subpath as closed. It must then create
a new subpath with the point (x, y) as the only point in the subpath.
The fill()
method must fill all the subpaths of the current path, using
fillStyle, and using
the non-zero winding number rule. Open subpaths must be implicitly
closed when being filled (without affecting the actual
subpaths).
Thus, if two overlapping but otherwise independent
subpaths have opposite windings, they cancel out and result in no
fill. If they have the same winding, that area just gets painted
once.
The stroke() method
must calculate the strokes of all the subpaths of the current path,
using the lineWidth,
lineCap, lineJoin, and (if
appropriate) miterLimit attributes, and
then fill the combined stroke area using the strokeStyle
attribute.
Since the subpaths are all stroked as one,
overlapping parts of the paths in one stroke operation are treated
as if their union was what was painted.
Paths, when filled or stroked, must be painted without affecting
the current path, and must be subject to shadow effects, global alpha, the clipping region, and global composition
operators. (Transformations affect the path when the path is
created, not when it is painted, though the stroke style is
still affected by the transformation during painting.)
Zero-length line segments must be pruned before stroking a
path. Empty subpaths must be ignored.
The clip()
method must create a new clipping region by calculating
the intersection of the current clipping region and the area
described by the current path, using the non-zero winding number
rule. Open subpaths must be implicitly closed when computing the
clipping region, without affecting the actual subpaths. The new
clipping region replaces the current clipping region.
When the context is initialized, the clipping region must be set
to the rectangle with the top left corner at (0,0) and the width and
height of the coordinate space.
The isPointInPath(x, y) method must
return true if the point given by the x and y coordinates passed to the method, when treated as
coordinates in the canvas coordinate space unaffected by the current
transformation, is inside the current path as determined by the
non-zero winding number rule; and must return false
otherwise. Points on the path itself are considered to be inside the
path. If either of the arguments is infinite or NaN, then the method
must return false.
10 Focus management
When a canvas is interactive, authors should include focusable
elements in the element's fallback content corresponding to each
focusable part of the canvas.
To indicate which focusable part of the canvas is currently
focused, authors should use the drawFocusRing() method,
passing it the element for which a ring is being drawn.
<ZZZ>
This method
only draws the focus ring if the element is focused or is a descendant
of the element with focus.
- shouldDraw = context .
drawFocusRing(element, [ canDrawCustom ])
-
If the given element is focused or a descendant of the element with focus, draws a focus ring around the
current path, following the platform conventions for focus
rings.
If the canDrawCustom argument is true, then
the focus ring is only drawn if the user has configured his system
to draw focus rings in a particular manner. (For example, high
contrast focus rings.)
Returns true if the given element is focused, the canDrawCustom argument is true, and the user has
not configured his system to draw focus rings in a particular
manner. Otherwise, returns false.
When the method returns true, the author is expected to
manually draw a focus ring.
The drawing path is used to form the focus ring provided that
drawing path contains a closed path. The drawing path is used to
form a best fit bounding rectangle in screen coordinates. The
bounding rectangle and drawing path may be used to enhance
accessibility properties [ARIA] for the
targeted element.
The drawFocusRing(element, [canDrawCustom])
method, when invoked, must run the following steps:
If the element is not focused or is not a
descendant of the element with whose context the method is
associated, then return false and abort these steps.
If supporting an accessibility API, implementors may use the drawing path to form a best fit rectangle in screen coordinates and apply it to the bounding rectangle of the associated accessible object.
-
If the user has requested the use of particular focus rings
(e.g. high-contrast focus rings), or if the canDrawCustom argument is absent or false, then
draw a focus ring of the appropriate style along the path,
following platform conventions, return false, and abort these
steps.
The focus ring should not be subject to the shadow effects, the global alpha, or the global composition
operators, but should be subject to the clipping region.
Return true.
11 Caret and selection management
When a canvas implementation is used to render
interactive content that contains a caret or selection, it is
essential that all users be able to follow the current caret or
selection position.
The setCaretSelectionRect() method should be used
to indicate the location of the last rendered caret position or selection position on the canvas, passing it the canvas fallback element
associated with the last drawn of either the caret position or the selection.
When drawing a blinking caret the author must adhere to the blink rates in systems that support this feature. User agents must provide the system caret blink rate to content authors. Default system caret blink rate settings are roughly once every 500 milliseconds.
To access the system caret blink rate in canvas use the caretBlinkRate() method
- success = context .
setCaretSelectionRect(element, x, y, w, h)
-
Returns true if the given element is focused or a document descendant of an element with focus. Otherwise, returns false.
- rate = context .
caretBlinkRate()
-
Returns the blink rate of the system in milliseconds if supported. Otherwise, returns -1 if it is unsupported by the system.
Screen magnifiers, used by low vision users, use this position to move the magnification point on the screen.
The setCaretSelectionRect(element, x, y, w, h)
method, when invoked, must run the following steps:
If element does not have selected content and is not focused return false and abort these steps.
If the element is not a descendant of the element with whose context the method is associated, then return false and abort these step.
Transform the given point (x, y), the width w, and the height h according to the current transformation matrix.
If the user agent supports a platform accessibility API the user agent must use the element, transformed coordinates and transformed bounding box, and provide it through the supported accessibility API implementation.
Return true.
If the user resizes or moves the user agent window the user agent report must reflect the revised (x, y, w, h) position (or rectangle) in the accessibility API mapping.
High blink rates may cause epileptic seizures in some users.
The caretBlinkRate()
method, when invoked, must run the following steps:
If the operating system supports a caret blink rate setting the user agent must return a long value in milliseconds.
If the operating system does not support a caret blink rate setting the user agent must return a long value less than zero.
When the caret blink rate value returned:
For blink rates greater than zero the author, when drawing a blinking caret, must reflect the blink rate returned by this method.
For a blink rate less than zero the author, when drawing a blinking caret, must determine the blink rate.
For a blink rate of zero the author should visibly render the caret.
Status: This example should be updated to remove compatibility code for non-compliant implementations:
This canvas element has a couple of checkboxes:
<canvas tabindex="-1" id="example" height="400" width="750" role="application">
<!-- Canvas Subtree acts as Shadow DOM that the browser maps to the platform accessibility API -->
<label id="labelA" for="showA"><input id="showA" role="checkbox" aria-labelledby="labelA" type="checkbox" /> Show "A"</label>
<label id="labelB" for="showB"><input id="showB" role="checkbox" aria-labelledby="labelB" type="checkbox" /> Show "B"</label>
<!-- ... -->
</canvas>
<script>
/*/
Canvas is a low level API and requires manual management of all interactivity.
The following example is quite verbose, and demonstrates the minimum of programming
necessary to enable a simple checkbox element within canvas.
/*/
function drawCheckbox(context, element, x, y, pathOnly) {
context.save();
context.font = '10px sans-serif';
context.textAlign = 'left';
context.textBaseline = 'middle';
var label = document.getElementById(element.getAttribute('aria-labelledby'));
var metrics = context.measureText(label.textContent);
if(pathOnly) {
var areaWidth = 15 + metrics.width;
var areaHeight = 10;
context.beginPath();
context.rect(x-5, y-5, areaWidth, areaHeight);
return;
}
context.beginPath();
context.strokeStyle = 'black';
context.rect(x-5, y-5, 10, 10);
context.stroke();
if (element.checked) {
context.fillStyle = 'black';
context.fill();
}
context.fillText(label.textContent, x+5, y);
// Draw the Focus Ring
var drawFocusManually = false;
if (document.activeElement == element || document.activeElementFocus == element && document.activeElement == context.canvas) {
try {
drawFocusManually = !context.drawFocusRing(element);
} catch(e) {
drawFocusManually = true;
}
}
if(drawFocusManually) {
context.beginPath();
context.rect(x-7, y-7, 12 + metrics.width+2, 14);
context.strokeStyle = 'silver';
context.stroke();
}
context.restore();
}
function drawBase() { /* ... */ }
function drawAs() { /* ... */ }
function drawBs() { /* ... */ }
function redraw() {
var canvas = document.getElementsByTagName('canvas')[0];
var context = canvas.getContext('2d');
var showA = document.getElementById('showA');
var showB = document.getElementById('showB');
context.clearRect(0, 0, canvas.width, canvas.height);
drawCheckbox(context, showA, 20, 40);
drawCheckbox(context, showB, 20, 60);
drawBase();
if (showA.checked) {
drawAs();
}
if (showB.checked) {
drawBs();
}
}
function processMouseCoords(event,element) {
var offsetLeft = 0, offsetTop = 0;
while(element) {
offsetLeft += element.offsetLeft >> 0;
offsetTop += element.offsetTop >> 0;
element = element.parentNode;
}
offsetLeft -= document.documentElement.scrollLeft;
offsetTop -= document.documentElement.scrollTop;
return { x: event.clientX - offsetLeft, y: event.clientY - offsetTop }
}
function processClick(event){
var canvas = document.getElementById('example');
var context = canvas.getContext('2d');
var coords = processMouseCoords(event,canvas);
var showA = document.getElementById('showA');
var showB = document.getElementById('showB');
var useRedraw = false;
if(event.target.type == 'checkbox') {
redraw();
return;
}
drawCheckbox(context, showA, 20, 40, true);
if (context.isPointInPath(coords.x, coords.y)) {
showA.checked = !(showA.checked);
showA.focus();
document.activeElementFocus = showA;
useRedraw = true;
}
drawCheckbox(context, showB, 20, 60, true);
if (context.isPointInPath(coords.x, coords.y)) {
showB.checked = !(showB.checked);
document.activeElementFocus = showB;
showB.focus();
useRedraw = true;
}
if(!useRedraw &&
(document.activeElementFocus != document.activeElement)) {
document.activeElementFocus = document.activeElement;
redraw();
}
if(useRedraw) redraw();
}
// Add the event listeners
document.getElementById('showA').addEventListener('focus', redraw, true);
document.getElementById('showB').addEventListener('focus', redraw, true);
document.getElementById('showA').addEventListener('blur', redraw, true);
document.getElementById('showB').addEventListener('blur', redraw, true);
document.getElementById('example').addEventListener('change', redraw, true);
document.getElementById('example').addEventListener('click', processClick, false);
redraw();
</script>
The caret position is the rectangular left edge of the caret position within an element having focus. The selection position is the rectangular left or right edge of the highlighted position that moves in response to a users selection of content such as when dragging a pointing device during a content selection operation. The right edge is used when moving the selection position to the right and the left edge is used when moving the position to the left.
</ZZZ>
11 Text
- context .
font [ = value ]
-
Returns the current font settings.
Can be set, to change the font. The syntax is the same as for
the CSS 'font' property; values that cannot be parsed as CSS font
values are ignored.
Relative keywords and lengths are computed relative to the font
of the canvas element.
- context .
textAlign [ = value ]
-
Returns the current text alignment settings.
Can be set, to change the alignment. The possible values are
start, end, left, right, and center. Other values are ignored. The default is
start.
- context .
textBaseline [ = value ]
-
Returns the current baseline alignment settings.
Can be set, to change the baseline alignment. The possible
values and their meanings are given below. Other values are
ignored. The default is alphabetic.
- context .
fillText(text, x, y [, maxWidth ] )
- context .
strokeText(text, x, y [, maxWidth ] )
-
Fills or strokes (respectively) the given text at the given
position. If a maximum width is provided, the text will be scaled
to fit that width if necessary.
- metrics = context .
measureText(text)
-
Returns a TextMetrics object with the metrics of the given text in the current font.
- metrics .
width
-
Returns the advance width of the text that was passed to the
measureText()
method.
The font IDL
attribute, on setting, must be parsed the same way as the 'font'
property of CSS (but without supporting property-independent style
sheet syntax like 'inherit'), and the resulting font must be
assigned to the context, with the 'line-height' component forced to
'normal', with the 'font-size' component converted to CSS pixels,
and with system fonts being computed to explicit values. If the new
value is syntactically incorrect (including using
property-independent style sheet syntax like 'inherit' or
'initial'), then it must be ignored, without assigning a new font
value. [CSS]
Font names must be interpreted in the context of the
canvas element's stylesheets; any fonts embedded using
@font-face must therefore be available once
they are loaded. (If a font is referenced before it is fully loaded,
then it must be treated as if it was an unknown font, falling back
to another as described by the relevant CSS specifications.) [CSSFONTS]
Only vector fonts should be used by the user agent; if a user
agent were to use bitmap fonts then transformations would likely
make the font look very ugly.
On getting, the font
attribute must return the serialized form of the current font of the context
(with no 'line-height' component). [CSSOM]
For example, after the following statement:
context.font = 'italic 400 12px/2 Unknown Font, sans-serif';
...the expression context.font would
evaluate to the string "italic 12px "Unknown Font", sans-serif". The
"400" font-weight doesn't appear because that is the default
value. The line-height doesn't appear because it is forced to
"normal", the default value.
When the context is created, the font of the context must be set
to 10px sans-serif. When the 'font-size' component is set to lengths
using percentages, 'em' or 'ex' units, or the 'larger' or 'smaller'
keywords, these must be interpreted relative to the computed value
of the 'font-size' property of the corresponding canvas
element at the time that the attribute is set. When the
'font-weight' component is set to the relative values 'bolder' and
'lighter', these must be interpreted relative to the computed value
of the 'font-weight' property of the corresponding
canvas element at the time that the attribute is
set. If the computed values are undefined for a particular case
(e.g. because the canvas element is not in a
Document), then the relative keywords must be
interpreted relative to the normal-weight 10px sans-serif
default.
The textAlign IDL
attribute, on getting, must return the current value. On setting, if
the value is one of start, end, left, right, or center, then the
value must be changed to the new value. Otherwise, the new value
must be ignored. When the context is created, the textAlign attribute must
initially have the value start.
The textBaseline
IDL attribute, on getting, must return the current value. On
setting, if the value is one of top, hanging, middle, alphabetic,
ideographic,
or bottom,
then the value must be changed to the new value. Otherwise, the new
value must be ignored. When the context is created, the textBaseline attribute
must initially have the value alphabetic.
The textBaseline
attribute's allowed keywords correspond to alignment points in the
font:

The keywords map to these alignment points as follows:
top
- The top of the em square
hanging
- The hanging baseline
middle
- The middle of the em square
alphabetic
- The alphabetic baseline
ideographic
- The ideographic baseline
bottom
- The bottom of the em square
The fillText() and
strokeText()
methods take three or four arguments, text, x, y, and optionally maxWidth, and render the given text at the given (x, y) coordinates ensuring that the text isn't wider
than maxWidth if specified, using the current
font, textAlign, and textBaseline
values. Specifically, when the methods are called, the user agent
must run the following steps:
If maxWidth is present but less than or
equal to zero, return without doing anything; abort these
steps.
Let font be the current font of the
context, as given by the font attribute.
Replace all the space
characters in text with U+0020 SPACE
characters.
Form a hypothetical infinitely wide CSS line box containing
a single inline box containing the text text,
with all the properties at their initial values except the 'font'
property of the inline box set to font and the
'direction' property of the inline box set to the
directionality of the canvas element. [CSS]
If the maxWidth argument was specified
and the hypothetical width of the inline box in the hypothetical
line box is greater than maxWidth CSS pixels,
then change font to have a more condensed font
(if one is available or if a reasonably readable one can be
synthesized by applying a horizontal scale factor to the font) or a
smaller font, and return to the previous step.
-
Let the anchor point be a point on the
inline box, determined by the textAlign and textBaseline values, as
follows:
Horizontal position:
- If
textAlign is left
- If
textAlign is start and the directionality of the
canvas element is 'ltr'
- If
textAlign is end and the directionality of the
canvas element is 'rtl'
- Let the anchor point's horizontal
position be the left edge of the inline box.
- If
textAlign is right
- If
textAlign is end and the directionality of the
canvas element is 'ltr'
- If
textAlign is start and the directionality of the
canvas element is 'rtl'
- Let the anchor point's horizontal
position be the right edge of the inline box.
- If
textAlign is center
- Let the anchor point's horizontal
position be half way between the left and right edges of the
inline box.
Vertical position:
- If
textBaseline is top
- Let the anchor point's vertical position
be the top of the em box of the first available font of the
inline box.
- If
textBaseline is hanging
- Let the anchor point's vertical position
be the hanging baseline of the first available font of the inline
box.
- If
textBaseline is middle
- Let the anchor point's vertical position
be half way between the bottom and the top of the em box of the
first available font of the inline box.
- If
textBaseline is alphabetic
- Let the anchor point's vertical position
be the alphabetic baseline of the first available font of the inline
box.
- If
textBaseline is ideographic
- Let the anchor point's vertical position
be the ideographic baseline of the first available font of the inline
box.
- If
textBaseline is bottom
- Let the anchor point's vertical position
be the bottom of the em box of the first available font of the
inline box.
-
Paint the hypothetical inline box as the shape given by the
text's glyphs, as transformed by the current transformation
matrix, and anchored and sized so that before applying the
current transformation
matrix, the anchor point is at (x, y) and each CSS pixel is
mapped to one coordinate space unit.
For fillText()
fillStyle must be
applied to the glyphs and strokeStyle must be
ignored. For strokeText() the reverse
holds and strokeStyle must be
applied to the glyph outlines and fillStyle must be
ignored.
Text is painted without affecting the current path, and is
subject to shadow effects, global alpha, the clipping region, and global composition
operators.
The measureText()
method takes one argument, text. When the method
is invoked, the user agent must replace all the space characters in text with
U+0020 SPACE characters, and then must form a hypothetical
infinitely wide CSS line box containing a single inline box
containing the text text, with all the
properties at their initial values except the 'font' property of the
inline element set to the current font of the context, as given by
the font attribute, and
must then return a new TextMetrics object with its
width attribute set to
the width of that inline box, in CSS pixels. [CSS]
The TextMetrics interface is used for the objects
returned from measureText(). It has one
attribute, width, which is set
by the measureText()
method.
Glyphs rendered using fillText() and strokeText() can spill out
of the box given by the font size (the em square size) and the width
returned by measureText() (the text
width). This version of the specification does not provide a way to
obtain the bounding box dimensions of the text. If the text is to be
rendered and removed, care needs to be taken to replace the entire
area of the canvas that the clipping region covers, not just the box
given by the em square height and measured text width.
A future version of the 2D context API may provide a
way to render fragments of documents, rendered using CSS, straight
to the canvas. This would be provided in preference to a dedicated
way of doing multiline layout.
12 Images
To draw images onto the canvas, the drawImage method
can be used.
This method can be invoked with three different sets of arguments:
drawImage(image, dx, dy)
drawImage(image, dx, dy, dw, dh)
drawImage(image, sx, sy, sw, sh, dx, dy, dw, dh)
Each of those three can take either an
HTMLImageElement, an HTMLCanvasElement, or
an HTMLVideoElement for the image
argument.
- context .
drawImage(image, dx, dy)
- context .
drawImage(image, dx, dy, dw, dh)
- context .
drawImage(image, sx, sy, sw, sh, dx, dy, dw, dh)
-
Draws the given image onto the canvas. The arguments are
interpreted as follows:
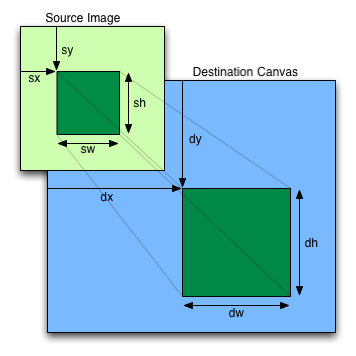
If the first argument isn't an img,
canvas, or video element, throws a
TYPE_MISMATCH_ERR exception. If the image has no
image data, throws an INVALID_STATE_ERR exception. If
the numeric arguments don't make sense (e.g. the destination is a
0×0 rectangle), throws an INDEX_SIZE_ERR
exception. If the image isn't yet fully decoded, then nothing is
drawn.
If not specified, the dw and dh arguments must default to the values of sw and sh, interpreted such that
one CSS pixel in the image is treated as one unit in the canvas
coordinate space. If the sx, sy, sw, and sh arguments are omitted, they must default to 0, 0,
the image's intrinsic width in image pixels, and the image's
intrinsic height in image pixels, respectively.
The image argument is an instance of either
HTMLImageElement, HTMLCanvasElement, or
HTMLVideoElement. If the image is
null, the implementation must raise a TYPE_MISMATCH_ERR
exception.
If the image argument is an
HTMLImageElement object that is not fully decodable, or if the image argument is an HTMLVideoElement
object whose readyState
attribute is either HAVE_NOTHING or HAVE_METADATA, then the
implementation must return without drawing anything.
If the image argument is an
HTMLCanvasElement object with either a horizontal
dimension or a vertical dimension equal to zero, then the
implementation must raise an INVALID_STATE_ERR
exception.
The source rectangle is the rectangle whose corners are the four
points (sx, sy), (sx+sw, sy), (sx+sw, sy+sh), (sx, sy+sh).
If one of the sw or sh
arguments is zero, the implementation must raise an
INDEX_SIZE_ERR exception.
The destination rectangle is the rectangle whose corners are the
four points (dx, dy),
(dx+dw, dy), (dx+dw, dy+dh), (dx, dy+dh).
When drawImage() is
invoked, the region of the image specified by the source rectangle
must be painted on the region of the canvas specified by the
destination rectangle, after applying the current transformation
matrix to the points of the destination rectangle.
The original image data of the source image must be used, not the
image as it is rendered (e.g. width and height attributes on the source
element have no effect). The image data must be processed in the
original direction, even if the dimensions given are negative.
This specification does not define the algorithm to
use when scaling the image, if necessary.
When a canvas is drawn onto itself, the drawing
model requires the source to be copied before the image is drawn
back onto the canvas, so it is possible to copy parts of a canvas
onto overlapping parts of itself.
If the original image data is a bitmap image, the value painted
at a point in the destination rectangle is computed by filtering the
original image data. The user agent may use any filtering algorithm
(for example bilinear interpolation or nearest-neighbor). When the
filtering algorithm requires a pixel value from outside the original
image data, it must instead use the value from the nearest edge
pixel. (That is, the filter uses 'clamp-to-edge' behavior.)
When the drawImage() method
is passed an animated image as its image
argument, the user agent must use the poster frame of the animation,
or, if there is no poster frame, the first frame of the
animation.
When the image argument is an
HTMLVideoElement, then the frame at the current
playback position must be used as the source image, and the
source image's dimensions must be the intrinsic width and
intrinsic height
of the media resource (i.e. after any aspect-ratio
correction has been applied).
Images are painted without affecting the current path, and are
subject to shadow effects, global alpha, the clipping region, and global composition
operators.
13 Pixel manipulation
- imagedata = context .
createImageData(sw, sh)
-
Returns an ImageData object with the given
dimensions in CSS pixels (which might map to a different number of
actual device pixels exposed by the object itself). All the pixels
in the returned object are transparent black.
- imagedata = context .
createImageData(imagedata)
-
Returns an ImageData object with the same
dimensions as the argument. All the pixels in the returned object
are transparent black.
Throws a NOT_SUPPORTED_ERR exception if the
argument is null.
- imagedata = context .
getImageData(sx, sy, sw, sh)
-
Returns an ImageData object containing the image
data for the given rectangle of the canvas.
Throws a NOT_SUPPORTED_ERR exception if any of the
arguments are not finite. Throws an INDEX_SIZE_ERR
exception if the either of the width or height arguments are
zero.
- imagedata .
width
- imagedata .
height
-
Returns the actual dimensions of the data in the ImageData object, in device pixels.
- imagedata .
data
-
Returns the one-dimensional array containing the data in RGBA order, as integers in the range 0 to 255.
- context .
putImageData(imagedata, dx, dy [, dirtyX, dirtyY, dirtyWidth, dirtyHeight ])
-
Paints the data from the given ImageData object
onto the canvas. If a dirty rectangle is provided, only the pixels
from that rectangle are painted.
The globalAlpha
and globalCompositeOperation
attributes, as well as the shadow attributes, are ignored for the
purposes of this method call; pixels in the canvas are replaced
wholesale, with no composition, alpha blending, no shadows,
etc.
If the first argument is null, throws a
TYPE_MISMATCH_ERR exception. Throws a
NOT_SUPPORTED_ERR exception if any of the other
arguments are not finite.
The createImageData()
method is used to instantiate new blank ImageData
objects. When the method is invoked with two arguments sw and sh, it must return an
ImageData object representing a rectangle with a width
in CSS pixels equal to the absolute magnitude of sw and a height in CSS pixels equal to the absolute
magnitude of sh. When invoked with a single imagedata argument, it must return an
ImageData object representing a rectangle with the same
dimensions as the ImageData object passed as the
argument. The ImageData object returned must be filled
with transparent black.
The getImageData(sx, sy, sw,
sh) method must return an
ImageData object representing the underlying pixel data
for the area of the canvas denoted by the rectangle whose corners are
the four points (sx, sy),
(sx+sw, sy), (sx+sw, sy+sh), (sx, sy+sh), in canvas
coordinate space units. Pixels outside the canvas must be returned
as transparent black. Pixels must be returned as non-premultiplied
alpha values.
If any of the arguments to createImageData() or
getImageData() are
infinite or NaN, or if the createImageData()
method is invoked with only one argument but that argument is null,
the method must instead raise a NOT_SUPPORTED_ERR
exception. If either the sw or sh arguments are zero, the method must instead raise
an INDEX_SIZE_ERR exception.
ImageData objects must be initialized so that their
width attribute
is set to w, the number of physical device
pixels per row in the image data, their height attribute is
set to h, the number of rows in the image data,
and their data
attribute is initialized to a CanvasPixelArray object
holding the image data. At least one pixel's worth of image data
must be returned.
The CanvasPixelArray object provides ordered,
indexed access to the color components of each pixel of the image
data. The data must be represented in left-to-right order, row by
row top to bottom, starting with the top left, with each pixel's
red, green, blue, and alpha components being given in that order for
each pixel. Each component of each device pixel represented in this
array must be in the range 0..255, representing the 8 bit value for
that component. The components must be assigned consecutive indices
starting with 0 for the top left pixel's red component.
The CanvasPixelArray object thus represents h×w×4 integers. The
length
attribute of a CanvasPixelArray object must return this
number.
The object's supported property indices are the
numbers in the range 0 .. h×w×4-1.
To determine the value of
an indexed property index, the user agent
must return the value of the indexth component
in the array.
To set the value of an
existing indexed property index to value
value, the value of the indexth component in the array must be set to value.
The width and height (w and h) might be different from the sw
and sh arguments to the above methods, e.g. if
the canvas is backed by a high-resolution bitmap, or if the sw and sh arguments are
negative.
The putImageData(imagedata, dx, dy, dirtyX, dirtyY, dirtyWidth, dirtyHeight) method writes data from
ImageData structures back to the canvas.
If any of the arguments to the method are infinite or NaN, the
method must raise a NOT_SUPPORTED_ERR exception.
If the first argument to the method is null, then the putImageData() method
must raise a TYPE_MISMATCH_ERR exception.
When the last four arguments are omitted, they must be assumed to
have the values 0, 0, the width member of the imagedata structure, and the height member of the imagedata structure, respectively.
When invoked with arguments that do not, per the last few
paragraphs, cause an exception to be raised, the putImageData() method
must act as follows:
-
Let dxdevice be the x-coordinate
of the device pixel in the underlying pixel data of the canvas
corresponding to the dx coordinate in the
canvas coordinate space.
Let dydevice be the y-coordinate
of the device pixel in the underlying pixel data of the canvas
corresponding to the dy coordinate in the
canvas coordinate space.
-
If dirtyWidth is negative, let dirtyX be dirtyX+dirtyWidth, and let dirtyWidth be equal to the absolute magnitude of
dirtyWidth.
If dirtyHeight is negative, let dirtyY be dirtyY+dirtyHeight, and let dirtyHeight be equal to the absolute magnitude of
dirtyHeight.
-
If dirtyX is negative, let dirtyWidth be dirtyWidth+dirtyX, and
let dirtyX be zero.
If dirtyY is negative, let dirtyHeight be dirtyHeight+dirtyY, and
let dirtyY be zero.
-
If dirtyX+dirtyWidth is greater than the width attribute of the imagedata argument, let dirtyWidth be the value of that width attribute, minus the
value of dirtyX.
If dirtyY+dirtyHeight is greater than the height attribute of the imagedata argument, let dirtyHeight be the value of that height attribute, minus the
value of dirtyY.
-
If, after those changes, either dirtyWidth
or dirtyHeight is negative or zero, stop these
steps without affecting the canvas.
Otherwise, for all integer values of x
and y where dirtyX ≤ x < dirtyX+dirtyWidth
and dirtyY ≤ y < dirtyY+dirtyHeight, copy the four channels of
the pixel with coordinate (x, y) in the imagedata data
structure to the pixel with coordinate (dxdevice+x,
dydevice+y) in the underlying pixel data of the
canvas.
The handling of pixel rounding when the specified coordinates do
not exactly map to the device coordinate space is not defined by
this specification, except that the following must result in no
visible changes to the rendering:
context.putImageData(context.getImageData(x, y, w, h), p, q);
...for any value of x, y,
w, and h and where p is the smaller of x and the sum
of x and w, and q is the smaller of y and the sum
of y and h; and except that
the following two calls:
context.createImageData(w, h);
context.getImageData(0, 0, w, h);
...must return ImageData objects with the same
dimensions, for any value of w and h. In other words, while user agents may round the
arguments of these methods so that they map to device pixel
boundaries, any rounding performed must be performed consistently
for all of the createImageData(), getImageData() and putImageData()
operations.
Due to the lossy nature of converting to and from
premultiplied alpha color values, pixels that have just been set
using putImageData() might be
returned to an equivalent getImageData() as
different values.
The current path, transformation matrix,
shadow attributes, global alpha, the clipping region, and global composition
operator must not affect the getImageData() and putImageData()
methods.
The data returned by getImageData() is at the
resolution of the canvas backing store, which is likely to not be
one device pixel to each CSS pixel if the display used is a high
resolution display.
In the following example, the script generates an
ImageData object so that it can draw onto it.
// canvas is a reference to a <canvas> element
var context = canvas.getContext('2d');
// create a blank slate
var data = context.createImageData(canvas.width, canvas.height);
// create some plasma
FillPlasma(data, 'green'); // green plasma
// add a cloud to the plasma
AddCloud(data, data.width/2, data.height/2); // put a cloud in the middle
// paint the plasma+cloud on the canvas
context.putImageData(data, 0, 0);
// support methods
function FillPlasma(data, color) { ... }
function AddCloud(data, x, y) { ... }
Here is an example of using getImageData() and putImageData() to
implement an edge detection filter.
<!DOCTYPE HTML>
<html>
<head>
<title>Edge detection demo</title>
<script>
var image = new Image();
function init() {
image.onload = demo;
image.src = "image.jpeg";
}
function demo() {
var canvas = document.getElementsByTagName('canvas')[0];
var context = canvas.getContext('2d');
// draw the image onto the canvas
context.drawImage(image, 0, 0);
// get the image data to manipulate
var input = context.getImageData(0, 0, canvas.width, canvas.height);
// get an empty slate to put the data into
var output = context.createImageData(canvas.width, canvas.height);
// alias some variables for convenience
// notice that we are using input.width and input.height here
// as they might not be the same as canvas.width and canvas.height
// (in particular, they might be different on high-res displays)
var w = input.width, h = input.height;
var inputData = input.data;
var outputData = output.data;
// edge detection
for (var y = 1; y < h-1; y += 1) {
for (var x = 1; x < w-1; x += 1) {
for (var c = 0; c < 3; c += 1) {
var i = (y*w + x)*4 + c;
outputData[i] = 127 + -inputData[i - w*4 - 4] - inputData[i - w*4] - inputData[i - w*4 + 4] +
-inputData[i - 4] + 8*inputData[i] - inputData[i + 4] +
-inputData[i + w*4 - 4] - inputData[i + w*4] - inputData[i + w*4 + 4];
}
outputData[(y*w + x)*4 + 3] = 255; // alpha
}
}
// put the image data back after manipulation
context.putImageData(output, 0, 0);
}
</script>
</head>
<body onload="init()">
<canvas></canvas>
</body>
</html>
14 Drawing model
When a shape or image is painted, user agents must follow these
steps, in the order given (or act as if they do):
Render the shape or image onto an infinite transparent black
bitmap, creating image A, as described in the
previous sections. For shapes, the current fill, stroke, and line
styles must be honored, and the stroke must itself also be
subjected to the current transformation matrix.
When shadows are drawn, render the shadow from
image A, using the current shadow styles,
creating image B.
When shadows are drawn, multiply the alpha
component of every pixel in B by globalAlpha.
When shadows are drawn, composite B within the clipping region over the
current canvas bitmap using the current composition
operator.
Multiply the alpha component of every pixel in A by globalAlpha.
Composite A within the clipping
region over the current canvas bitmap using the current
composition operator.
15 Examples
This section is non-normative.
Here is an example of a script that uses canvas to draw pretty
glowing lines.
<canvas width="800" height="450"></canvas>
<script>
var context = document.getElementsByTagName('canvas')[0].getContext('2d');
var lastX = context.canvas.width * Math.random();
var lastY = context.canvas.height * Math.random();
var hue = 0;
function line() {
context.save();
context.translate(context.canvas.width/2, context.canvas.height/2);
context.scale(0.9, 0.9);
context.translate(-context.canvas.width/2, -context.canvas.height/2);
context.beginPath();
context.lineWidth = 5 + Math.random() * 10;
context.moveTo(lastX, lastY);
lastX = context.canvas.width * Math.random();
lastY = context.canvas.height * Math.random();
context.bezierCurveTo(context.canvas.width * Math.random(),
context.canvas.height * Math.random(),
context.canvas.width * Math.random(),
context.canvas.height * Math.random(),
lastX, lastY);
hue = hue + 10 * Math.random();
context.strokeStyle = 'hsl(' + hue + ', 50%, 50%)';
context.shadowColor = 'white';
context.shadowBlur = 10;
context.stroke();
context.restore();
}
setInterval(line, 50);
function blank() {
context.fillStyle = 'rgba(0,0,0,0.1)';
context.fillRect(0, 0, context.canvas.width, context.canvas.height);
}
setInterval(blank, 40);
</script>
References
All references are normative unless marked "Non-normative".
- [BEZIER]
- Courbes à poles, P. de Casteljau. INPI, 1959.
- [CSS]
- Cascading Style Sheets Level 2
Revision 1, B. Bos, T. Çelik, I.
Hickson, H. Lie. W3C.
- [CSSCOLOR]
- CSS Color
Module Level 3, T. Çelik, C. Lilley, L.
Baron. W3C.
- [CSSFONTS]
- CSS Fonts
Module Level 3, J. Daggett. W3C.
- [CSSOM]
- Cascading Style Sheets
Object Model (CSSOM), A. van Kesteren. W3C.
- [HTML5]
-
HTML5,
I. Hickson. W3C.
- [PORTERDUFF]
- Compositing
Digital Images, T. Porter, T. Duff. In Computer
graphics, volume 18, number 3, pp. 253-259. ACM Press, July
1984.
- [WEBIDL]
- Web
IDL, C. McCormack. W3C.
Acknowledgements
For a full list of acknowledgements, please see the HTML5
specification. [HTML5]

